译 - CRUSH: Controlled, Scalable, Decentralized Placement of Replicated Data

译作: 可控的、可扩展的、分布式的副本数据放置算法，论文原文 。 该论文于 2006 年 11 月发布于 SC2006 。

CRUSH 是一种用于大规模分布式存储系统的数据分布算法，它通过伪随机函数将数据对象映射到存储设备上，无需依赖中央目录。CRUSH 算法设计考虑了系统的动态性，支持在添加或移除存储设备时高效地重组数据，并最小化不必要的数据移动。此外，CRUSH 支持多种数据复制和可靠性机制，并允许根据用户定义的策略进行数据分布，这些策略能够在故障域之间有效地分离副本，增强数据安全性。

CRUSH 的核心是其层级集群图，该图描述了存储集群的物理和逻辑结构，并通过一系列规则来确定数据的放置位置。CRUSH 算法通过将数据均匀分布在加权设备上，保持存储和设备带宽资源的平衡利用。算法还考虑了设备的故障和过载情况，能够在设备发生故障或过载时重新分配数据，避免数据丢失并优化系统性能。

CRUSH 的映射性能高效，计算复杂度为 O(logn) ，适用于管理大规模（多 PB 级）的存储系统。CRUSH的设计不仅提高了系统的可扩展性和性能，还通过智能的数据分布策略提高了系统的可靠性和数据安全性。

摘要

Emerging large-scale distributed storage systems are faced with the task of distributing petabytes of data among tens or hundreds of thousands of storage devices. Such systems must evenly distribute data and workload to efficiently utilize available resources and maximize system performance, while facilitating system growth and managing hardware failures. We have developed CRUSH, a scalable pseudorandom data distribution function designed for distributed object-based storage systems that efficiently maps data objects to storage devices without relying on a central directory. Because large systems are inherently dynamic, CRUSH is designed to facilitate the addition and removal of storage while minimizing unnecessary data movement. The algorithm accommodates a wide variety of data replication and reliability mechanisms and distributes data in terms of userdefined policies that enforce separation of replicas across failure domains.

新兴的大规模分布式存储系统面临着在数万甚至数十万个存储设备之间分发 PB 级数据的任务。此类系统必须均匀分布数据和工作负载，以高效利用可用资源并最大化系统性能，同时促进系统增长并管理硬件故障。我们开发了 CRUSH，这是一种可扩展的伪随机数据分布函数，专为基于对象的分布式存储系统而设计，它无需依赖中央目录即可高效地将数据对象映射到存储设备。由于大型系统本质上是动态的，CRUSH 旨在方便存储的添加和移除，同时最大限度地减少不必要的数据移动。该算法兼容各种数据复制和可靠性机制，并根据用户定义的策略分发数据，这些策略强制在故障域之间分离副本。

1、介绍

Object-based storage is an emerging architecture that promises improved manageability, scalability, and performance [Azagury et al. 2003]. Unlike conventional blockbased hard drives, object-based storage devices (OSDs) manage disk block allocation internally, exposing an interface that allows others to read and write to variably-sized, named objects. In such a system, each file’s data is typically striped across a relatively small number of named objects distributed throughout the storage cluster. Objects are replicated across multiple devices (or employ some other data redundancy scheme) in order to protect against data loss in the presence of failures. Object-based storage systems simplify data layout by replacing large block lists with small object lists and distributing the low-level block allocation problem. Although this vastly improves scalability by reducing file allocation metadata and complexity, the funda mental task of distributing data among thousands of storage devices—typically with varying capacities and performance characteristics—remains.

基于对象的存储是一种新兴架构，有望提升可管理性、可扩展性和性能 [Azagury et al. 2003]。与传统的基于块的硬盘不同，基于对象的存储设备 (OSD) 在内部管理磁盘块分配，并公开一个接口，允许其他设备读写大小可变的命名对象。在这样的系统中，每个文件的数据通常被条带化到分布在整个存储集群中的相对较少的命名对象上。对象会在多个设备上复制（或采用其他数据冗余方案），以防止在发生故障时丢失数据。基于对象的存储系统通过将大型块列表替换为小型对象列表并分散低级块分配问题来简化数据布局。虽然这通过减少文件分配元数据和复杂性极大地提高了可扩展性，但其根本在数千个存储设备（通常具有不同的容量和性能特征）之间分配数据的脑力任务仍然存在。

Most systems simply write new data to underutilized devices. The fundamental problem with this approach is that data is rarely, if ever, moved once it is written. Even a perfect distribution will become imbalanced when the storage system is expanded, because new disks either sit empty or contain only new data. Either old or new disks may be busy, depending on the system workload, but only the rarest of conditions will utilize both equally to take full advantage of available resources.

大多数系统只是将新数据写入未充分利用的设备。这种方法的根本问题在于，数据一旦写入，就很少（甚至根本不会）移动。即使是完美的分布，在存储系统扩展时也会变得不平衡，因为新磁盘要么空着，要么只包含新数据。根据系统工作负载，新旧磁盘都可能处于繁忙状态，但只有在极少数情况下，两者才能均衡利用，从而充分利用可用资源。

A robust solution is to distribute all data in a system randomly among available storage devices. This leads to a probabilistically balanced distribution and uniformly mixes old and new data together. When new storage is added, a random sample of existing data is migrated onto new storage devices to restore balance. This approach has the critical advantage that, on average, all devices will be similarly loaded, allowing the system to perform well under any potential workload [Santos et al. 2000]. Furthermore, in a large storage system, a single large file will be randomly distributed across a large set of available devices, providing a high level of parallelism and aggregate bandwidth. However, simple hashbased distribution fails to cope with changes in the number of devices, incurring a massive reshuffling of data. Further, existing randomized distribution schemes that decluster replication by spreading each disk’s replicas across many other devices suffer from a high probability of data loss from coincident device failures.

一种稳健的解决方案是将系统中的所有数据随机分布在可用的存储设备中。这将实现概率平衡的分布，并均匀地混合新旧数据。添加新存储时，现有数据的随机样本将迁移到新的存储设备上以恢复平衡。这种方法的关键优势在于，平均而言，所有设备的负载都相似，从而使系统在任何潜在工作负载下都能表现良好 [Santos et al. 2000]。此外，在大型存储系统中，单个大文件将随机分布在大量可用设备上，从而提供高水平的并行性和总带宽。然而，简单的基于哈希的分布无法应对设备数量的变化，会导致数据大规模重新排列。此外，现有的随机分布方案通过将每个磁盘的副本分散到许多其他设备上来分散复制，由于设备同时发生故障，数据丢失的概率很高。

We have developed CRUSH (Controlled Replication Under Scalable Hashing), a pseudo-random data distribution algorithm that efficiently and robustly distributes object replicas across a heterogeneous, structured storage cluster. CRUSH is implemented as a pseudo-random, deterministic function that maps an input value, typically an object or object group identifier, to a list of devices on which to store object replicas. This differs from conventional approaches in that data placement does not rely on any sort of per-file or per-object directory—CRUSH needs only a compact, hierarchical description of the devices comprising the storage cluster and knowledge of the replica placement policy. This approach has two key advantages: first, it is completely distributed such that any party in a large system can independently calculate the location of any object; and second, what little metadata is required is mostly static, changing only when devices are added or removed.

我们开发了 CRUSH（可扩展哈希下的受控复制），这是一种伪随机数据分布算法，能够在异构结构化存储集群中高效且稳健地分布对象副本。CRUSH 实现为一个伪随机的确定性函数，它将输入值（通常是对象或对象组标识符）映射到用于存储对象副本的设备列表。这与传统方法的不同之处在于，数据放置不依赖于任何类型的文件或对象目录——CRUSH 只需要对组成存储集群的设备进行紧凑的分层描述，以及副本放置策略的知识。这种方法有两个关键优势：首先，它是完全分布式的，大型系统中的任何一方都可以独立计算任何对象的位置；其次，这与传统方法的不同之处在于，数据放置不依赖于任何类型的每个文件或每个对象目录 - CRUSH 只需要少量紧凑的元数据，这些元数据大多是静态的，仅在添加或删除设备时更改。

CRUSH is designed to optimally distribute data to utilize available resources, efficiently reorganize data when storage devices are added or removed, and enforce flexible constraints on object replica placement that maximize data safety in the presence of coincident or correlated hardware failures. A wide variety of data safety mechanisms are supported, including n-way replication (mirroring), RAID parity schemes or other forms of erasure coding, and hybrid approaches (e. g., RAID-10). These features make CRUSH ideally suited for managing object distribution in extremely large (multi-petabyte) storage systems where scalability, performance, and reliability are critically important.

CRUSH 的设计目标是以最优方式分配数据以充分利用可用资源，在添加或移除存储设备时高效地重组数据，并对对象副本的放置施加灵活的约束，从而在发生同时或相关的硬件故障时最大限度地保障数据安全。它支持多种数据安全机制，包括多路复制（镜像）、RAID 奇偶校验方案或其他形式的纠删码，以及混合方案（例如 RAID-10）。这些特性使 CRUSH 非常适合在可扩展性、性能和可靠性至关重要的超大规模（多 PB）存储系统中管理对象分布。

2、相关工作

Object-based storage has recently garnered significant interest as a mechanism for improving the scalability of storage systems. A number of research and production file systems have adopted an object-based approach, including the seminal NASD file system [Gobioff et al. 1997], the Panasas file system [Nagle et al. 2004], Lustre [Braam 2004], and others [Rodeh and Teperman 2003; Ghemawat et al. 2003]. Other block-based distributed file systems like GPFS [Schmuck and Haskin 2002] and Federated Array of Bricks (FAB) [Saito et al. 2004] face a similar data distribution challenge. In these systems a semi-random or heuristicbased approach is used to allocate new data to storage devices with available capacity, but data is rarely relocated to maintain a balanced distribution over time. More importantly, all of these systems locate data via some sort of metadata directory, while CRUSH relies instead on a compact cluster description and deterministic mapping function. This distinction is most significant when writing data, as systems utilizing CRUSH can calculate any new data’s storage target without consulting a central allocator. The Sorrento [Tang et al. 2004] storage system’s use of consistent hashing [Karger et al. 1997] most closely resembles CRUSH, but lacks support for controlled weighting of devices, a wellbalanced distribution of data, and failure domains for improving data safety.

作为一种提升存储系统可扩展性的机制，基于对象的存储近年来引起了广泛关注。许多研究和生产文件系统都采用了基于对象的方法，包括开创性的 NASD 文件系统 [Gobioff et al. 1997]、Panasas 文件系统 [Nagle et al. 2004]、Lustre [Braam 2004] 以及其他文件系统 [Rodeh and Teperman 2003; Ghemawat et al. 2003]。其他基于块的分布式文件系统，例如 GPFS [Schmuck and Haskin 2002] 和 Federated Array of Bricks (FAB) [Saito et al. 2004]，也面临着类似的数据分布挑战。在这些系统中，人们采用半随机或启发式方法将新数据分配到具有可用容量的存储设备中，但很少重新定位数据以保持长期均衡分布。更重要的是，所有这些系统都通过某种元数据目录来定位数据，而 CRUSH 则依赖于紧凑的集群描述和确定性映射函数。这种区别在写入数据时最为明显，因为使用 CRUSH 的系统无需咨询中央分配器即可计算任何新数据的存储目标。Sorrento [Tang et al. 2004] 存储系统对一致性哈希 [Karger et al. 1997] 的使用与 CRUSH 最为相似，但缺乏对设备权重控制、数据均衡分布以及故障域（用于提高数据安全性）的支持。

Although the data migration problem has been studied extensively in the context of systems with explicit allocation maps [Anderson et al. 2001; Anderson et al. 2002], such approaches have heavy metadata requirements that functional approaches like CRUSH avoid. Choy, et al. [1996] describe algorithms for distributing data over disks which move an optimal number of objects as disks are added, but do not support weighting, replication, or disk removal. Brinkmann, et al. [2000] use hash functions to distribute data to a heterogeneous but static cluster. SCADDAR [Goel et al. 2002] addresses the addition and removal of storage, but only supports a constrained subset of replication strategies. None of these approaches include CRUSH’s flexibility or failure do mains for improved reliability.

尽管数据迁移问题已在具有显式分配图的系统环境中得到广泛研究 [Anderson 等人 2001；Anderson 等人 2002]，但此类方法对元数据的要求很高，而 CRUSH 等函数式方法则可避免这种情况。Choy 等人 [1996] 描述了在磁盘上分配数据的算法，这些算法会在添加磁盘时移动最优数量的对象，但不支持加权、复制或磁盘移除。Brinkmann 等人 [2000] 使用哈希函数将数据分发到异构但静态的集群。SCADDAR [Goel 等人 2002] 解决了存储的添加和移除问题，但仅支持有限的复制策略子集。这些方法都不具备 CRUSH 的灵活性或故障域，因此无法提高可靠性。

CRUSH most closely resembles the RUSH [Honicky and Miller 2004] family of algorithms upon which it is based. RUSH remains the only existing set of algorithms in the literature that utilizes a mapping function in place of explicit metadata and supports the efficient addition and removal of weighted devices. Despite these basic properties, a number of issues make RUSH an insufficient solution in practice. CRUSH fully generalizes the useful elements of RUSHp and RUSHt while resolving previously unaddressed reliability and replication issues, and offering improved performance and flexibility.

CRUSH 与其所基于的 RUSH [Honicky and Miller 2004] 算法系列最为相似。RUSH 仍然是文献中唯一一组使用映射函数代替显式元数据并支持高效添加和移除加权设备的算法。尽管具备这些基本特性，但一些问题使得 RUSH 在实践中无法提供足够的解决方案。CRUSH 充分概括了 RUSHp 和 RUSHt 的实用元素，同时解决了先前未解决的可靠性和复制问题，并提供了更高的性能和灵活性。

3、CRUSH 算法

The CRUSH algorithm distributes data objects among storage devices according to a per-device weight value, approximating a uniform probability distribution. The distribution is controlled by a hierarchical cluster map representing the available storage resources and composed of the logical elements from which it is built. For example, one might describe a large installation in terms of rows of server cabinets, cabinets filled with disk shelves, and shelves filled with storage devices. The data distribution policy is defined in terms of placement rules that specify how many replica targets are chosen from the cluster and what restrictions are imposed on replica placement. For example, one might specify that three mirrored replicas are to be placed on devices in different physical cabinets so that they do not share the same electrical circuit.

CRUSH 算法根据每个设备的权重值将数据对象分布在存储设备之间，近似于均匀的概率分布。该分布由表示可用存储资源的层级集群图控制，该图由构建集群的逻辑元素组成。例如，可以用成排的服务器机柜、装满磁盘架的机柜以及装满存储设备的机架来描述大型设施。数据分布策略根据放置规则定义，这些规则指定从集群中选择多少个副本目标以及对副本放置施加哪些限制。例如，可以指定将三个镜像副本放置在不同物理机柜中的设备上，以使它们不共享同一电路。

Given a single integer input value x, CRUSH will output an ordered list R of n distinct storage targets. CRUSH utilizes a strong multi-input integer hash function whose inputs include x, making the mapping completely deterministic and independently calculable using only the cluster map, placement rules, and x. The distribution is pseudo-random in that there is no apparent correlation between the resulting output from similar inputs or in the items stored on any storage device. We say that CRUSH generates a declustered distribution of replicas in that the set of devices sharing replicas for one item also appears to be independent of all other items.

给定一个整数输入值 x，CRUSH 将输出一个包含 n 个不同存储目标的有序列表 R。CRUSH 使用一个强多输入整数哈希函数，其输入包含 x，从而使映射具有完全确定性，并且仅使用集群映射、放置规则和 x 即可独立计算。该分布是伪随机的，因为相似输入的结果输出之间以及存储在任何存储设备上的项目之间没有明显的相关性。我们称 CRUSH 生成非集群副本分布，因为共享某个项目的副本的设备集似乎也与所有其他项目无关。

3.1、层次聚类图

The cluster map is composed of devices and buckets, both of which have numerical identifiers and weight values associated with them. Buckets can contain any number of devices or other buckets, allowing them to form interior nodes in a storage hierarchy in which devices are always at the leaves. Storage devices are assigned weights by the administrator to control the relative amount of data they are responsible for storing. Although a large system will likely contain devices with a variety of capacity and performance characteristics, randomized data distributions statistically correlate device utilization with workload, such that device load is on average proportional to the amount of data stored. This results in a one-dimensional placement metric, weight, which should be derived from the device’s capabilities. Bucket weights are defined as the sum of the weights of the items they contain.

集群图由设备和存储桶组成，两者都具有与之关联的数字标识符和权重值。存储桶可以包含任意数量的设备或其他存储桶，从而允许它们构成存储层次结构中的内部节点，其中设备始终位于叶子节点。管理员会为存储设备分配权重，以控制其负责存储的相对数据量。虽然大型系统可能包含具有各种容量和性能特征的设备，但随机数据分布在统计上与设备存储桶可以包含任意数量的设备或其他具有工作负载的存储桶利用率，使得设备负载平均与存储的数据量成正比。这会产生一个一维的放置指标——权重，该指标应根据设备的功能得出。存储桶权重定义为其所含项目权重的总和。

Buckets can be composed arbitrarily to construct a hierarchy representing available storage. For example, one might create a cluster map with “shelf” buckets at the lowest level to represent sets of identical devices as they are installed, and then combine shelves into “cabinet” buckets to group together shelves that are installed in the same rack. Cabinets might be further grouped into “row” or “room” buckets for a large system. Data is placed in the hierarchy by recursively selecting nested bucket items via a pseudo-random hash-like function. In contrast to conventional hashing techniques, in which any change in the number of target bins (devices) results in a massive reshuffling of bin contents, CRUSH is based on four different bucket types, each with a different selection algorithm to address data movement resulting from the addition or removal of devices and overall computational complexity.

存储桶可以任意组合，以构建表示可用存储的层级结构。例如，可以创建一个集群图，最低层级为“机架”存储桶，用于表示已安装的相同设备集合；然后将机架组合成“机柜”存储桶，将安装在同一机架中的机架归为一组。对于大型系统，机柜可以进一步分组为“行”或“房间”存储桶。数据通过伪随机哈希函数递归选择嵌套存储桶项，从而放置在层级结构中。传统哈希技术中，目标存储箱（设备）数量的任何变化都会导致存储箱内容的大规模重新排列。相比之下，CRUSH 基于四种不同的存储桶类型，每种类型都采用不同的选择算法来处理因添加或移除设备而导致的数据移动以及整体计算复杂度。

3.2、副本放置

CRUSH is designed to distribute data uniformly among weighted devices to maintain a statistically balanced utilization of storage and device bandwidth resources. The placement of replicas on storage devices in the hierarchy can also have a critical effect on data safety. By reflecting the underlying physical organization of the installation, CRUSH can model—and thereby address—potential sources of correlated device failures. Typical sources include physical proximity, a shared power source, and a shared network. By encoding this information into the cluster map, CRUSH placement policies can separate object replicas across different failure domains while still maintaining the desired distribution. For example, to address the possibility of concurrent failures, it may be desirable to ensure that data replicas are on devices in different shelves, racks, power supplies, controllers, and/or physical locations.

CRUSH 旨在将数据均匀地分布在加权设备之间，以保持存储和设备带宽资源的统计平衡利用率。副本在层级结构中存储设备上的放置位置也会对数据安全产生关键影响。通过反映设备底层的物理组织结构，CRUSH 可以建模并由此解决相关设备故障的潜在根源。典型的根源包括物理邻近性、共享电源和共享网络。通过将这些信息编码到集群映射中，CRUSH 放置策略可以将对象副本分散到不同的故障域中，同时仍保持所需的分布。例如，为了应对并发故障的可能性，可能需要确保数据副本位于不同机架、机柜、电源、控制器和/或物理位置的设备上。

In order to accommodate the wide variety of scenarios in which CRUSH might be used, both in terms of data replication strategies and underlying hardware configurations, CRUSH defines placement rules for each replication strategy or distribution policy employed that allow the storage system or administrator to specify exactly how object replicas are placed. For example, one might have a rule selecting a pair of targets for 2-way mirroring, one for selecting three targets in two different data centers for 3-way mirroring, one for RAID-4 over six storage devices, and so on1.

为了适应 CRUSH 的各种应用场景，包括数据复制策略和底层硬件配置，CRUSH 为每种复制策略或分发策略定义了放置规则，允许存储系统或管理员精确指定对象副本的放置方式。例如，一个规则可以选择一对目标进行双向镜像，一个规则可以选择位于两个不同数据中心的三个目标进行三向镜像，一个规则可以选择用于六个存储设备上的 RAID-4 镜像，等等。

Each rule consists of a sequence of operations applied to the hierarchy in a simple execution environment, presented as pseudocode in Algorithm 1. The integer input to the CRUSH function, x, is typically an object name or other identifier, such as an identifier for a group of objects whose replicas will be placed on the same devices. The take(a) operation selects an item (typically a bucket) within the storage hierarchy and assigns it to the vector i, which serves as an input to subsequent operations. The select(n,t) operation iterates over each element i ∈ i, and chooses n distinct items of type t in the subtree rooted at that point. Storage devices have a known, fixed type, and each bucket in the system has a type field that is used to distinguish between classes of buckets (e. g., those representing “rows” and those representing “cabinets”). For each i ∈ i, the select(n,t) call iterates over the r ∈ 1,…,n items requested and recursively descends through any intermediate buckets, pseudo-randomly selecting a nested item in each bucket using the function c(r,x) (defined for each kind of bucket in Section 3.4), until it finds an item of the requested type t. The resulting n| i| distinct items are placed back into the input i and either form the input for a subsequent select(n,t) or are moved into the result vector with an emit operation.

每条规则由应用于简单执行环境中的层次结构的一系列操作组成，呈现如算法 1 中的伪代码所示。CRUSH 函数的整数输入 x 通常是对象名称或其他标识符，例如，一组对象的标识符，这些对象的副本将放置在相同的设备上。take(a) 操作在存储层次结构中选择一个项目（通常是一个存储桶），并将其分配给向量 i，该向量作为后续操作的输入。select(n,t) 操作迭代每个元素 i ∈ i，并在以该点为根的子树中选择 n 个不同的类型为 t 的项目。存储设备具有已知的固定类型，系统中的每个存储桶都有一个 type 字段用于区分存储桶的类别（例如，表示“行”的存储桶和表示“柜子”的存储桶）。对于每个 i ∈ i，select(n,t) 调用会遍历请求的 r ∈ 1, …, n 个项目，并以递归方式向下遍历任何中间存储桶，使用函数 c(r, x)（在第 3.4 节中为每种类型的存储桶定义）伪随机地在每个存储桶中选择一个嵌套项目，直到找到所需类型为 t 的项目。将得到的 n| i| 个不同项目放回输入 i 中，并形成后续 select(n,t) 的输入，或者通过 emit 操作将其移入结果向量。

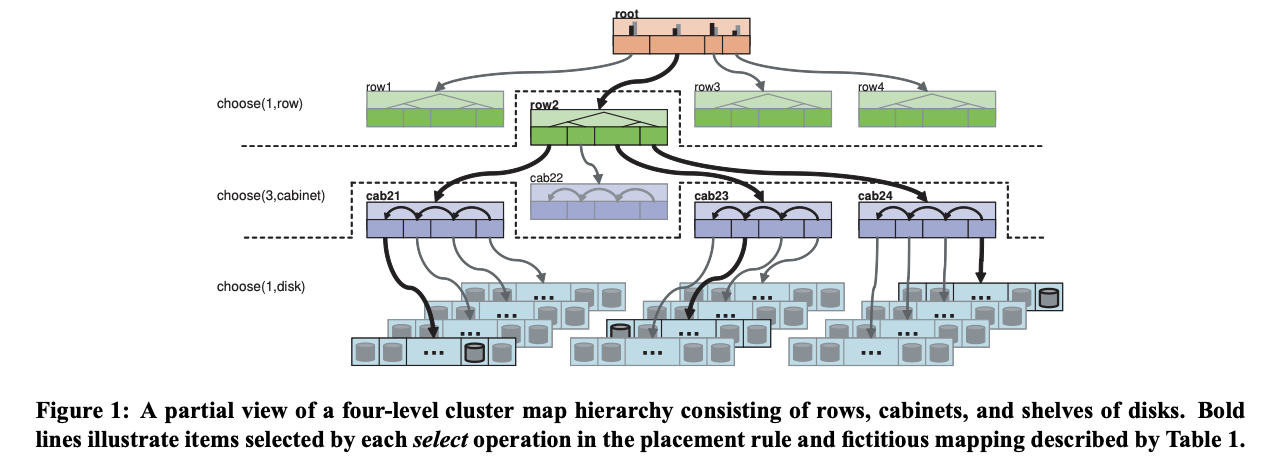
As an example, the rule defined in Table 1 begins at the root of the hierarchy in Figure 1 and with the first select(1,row) chooses a single bucket of type “row” (it selects row2). The subsequent select(3,cabinet) chooses three distinct cabinets nested beneath the previously selected row2 (cab21,cab23,cab24), while the final select(1,disk) iterates over the three cabinet buckets in the input vector and chooses a single disk nested beneath each of them. The final result is three disks spread over three cabinets, but all in the same row. This approach thus allows replicas to be simultaneously separated across and constrained within container types (e. g. rows, cabinets, shelves), a useful property for both reliability and performance considerations. Rules consisting of multiple take, emit blocks allow storage targets to be explicitly drawn from different pools of storage, as might be expected in remote replication scenarios (in which one replica is stored at a remote site) or tiered installations (e. g., fast, near-line storage and slower, higher-capacity arrays).

举例来说，表 1 中定义的规则从图 1 中层次结构的根开始，第一个 select(1,row) 选择类型为“row”的单个存储桶（它选择了 row2）。随后的 select(3,cabinet) 选择嵌套在先前选择的 row2 下方的三个不同的机柜（cab21、cab23、cab24），而最后一个 select(1,disk) 则在输入向量中的三个机柜存储桶上进行迭代，并选择嵌套在每个存储桶下方的单个磁盘。最终结果是三个磁盘分布在三个机柜上，但都在同一行中。因此，这种方法允许副本同时在容器类型（例如行、机柜、架子）内分离和约束，这对于可靠性和性能考虑都很有用。由多个 take、emit 块组成的规则允许从不同的存储池中明确提取存储目标，就像在远程复制场景（其中一个副本存储在远程站点）或分层安装（例如，快速、近线存储和较慢、更高容量的阵列）中所预期的那样。

3.2.1、碰撞、故障和过载

The select(n,t) operation may traverse many levels of the storage hierarchy in order to locate n distinct items of the specified type t nested beneath its starting point, a recursive process partially parameterized by r = 1,…,n, the replica number being chosen. During this process, CRUSH may reject and reselect items using a modified input r ′ for three different reasons: if an item has already been selected in the current set (a collision—the select(n,t) result must be distinct), if a device is failed, or if a device is overloaded. Failed or overloaded devices are marked as such in the cluster map, but left in the hierarchy to avoid unnecessary shifting of data. CRUSH’s selectively diverts a fraction of an overloaded device’s data by pseudo-randomly rejecting with the probability specified in the cluster map—typically related to its reported over-utilization. For failed or overloaded devices, CRUSH uniformly redistributes items across the storage cluster by restarting the recursion at the beginning of the select(n,t) (see Algorithm 1 line 11). In the case of collisions, an alternate r′ is used first at inner levels of the recursion to attempt a local search (see Algorithm 1 line 14) and avoid skewing the overall data distribution away from subtrees where collisions are more probable (e. g., where buckets are smaller than n).

select(n,t) 操作可能会遍历存储层级的多个层级，以便在其起始点下方找到嵌套的 n 个指定类型 t 的不同项目。这是一个递归过程，部分参数为 r = 1, …, n，其中副本数量已选定。在此过程中，CRUSH 可能会出于以下三种不同原因，使用修改后的输入 r 拒绝并重新选择项目：如果某个项目已在当前集合中被选中（发生冲突——select(n,t) 的结果必须不同）、设备发生故障或设备过载。故障或过载的设备会在集群映射中被标记，但仍会保留在层级结构中，以避免不必要的数据移动。 CRUSH 会通过伪随机拒绝的方式，选择性地转移过载设备的部分数据，其概率通常与集群图中指定的过载率相关。对于故障或过载的设备，CRUSH 会通过在 select(n,t) 的开头重新启动递归，在存储集群中均匀地重新分配项目（参见算法 1 第 11 行）。如果发生冲突，则首先在递归的内层使用备用方案，尝试进行局部搜索（参见算法 1 第 14 行），以避免整体数据分布偏离更可能发生冲突的子树（例如，桶小于 n 的情况）。

3.2.2、副本等级

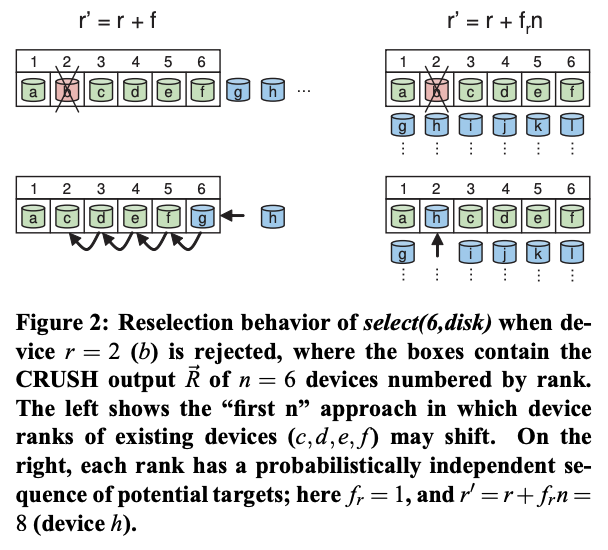
Parity and erasure coding schemes have slightly different placement requirements than replication. In primary copy replication schemes, it is often desirable after a failure for a previous replica target (that already has a copy of the data) to become the new primary. In such situations, CRUSH can use the “first n” suitable targets by reselecting using r ′ = r + f , where f is the number of failed placement attempts by the current select(n,t) (see Algorithm 1 line 16). With parity and erasure coding schemes, however, the rank or position of a storage device in the CRUSH output is critical because each target stores different bits of the data object. In particular, if a storage device fails, it should be replaced in CRUSH’s output list R in place, such that other devices in the list retain the same rank (i. e. position in R, see Figure 2). In such cases, CRUSH reselects using r ′ = r + frn, where fr is the number of failed attempts on r, thus defining a sequence of candidates for each replica rank that are probabilistically independent of others’ failures. In contrast, RUSH has no special handling of failed devices; like other existing hashing distribution functions, it implicitly assumes the use of a “first n” approach to skip over failed devices in the result, making it unweildly for parity schemes.

奇偶校验和纠删码方案的放置要求与复制略有不同。在主副本复制方案中，通常希望在发生故障后，让先前的副本目标（已拥有数据副本）成为新的主副本。在这种情况下，CRUSH 可以通过使用 r= r + f 重新选择来使用“前 n 个”合适的目标，其中 f 是当前 select(n,t) 尝试放置失败的次数（参见算法 1 第 16 行）。然而，对于奇偶校验和纠删码方案，存储设备在 CRUSH 输出中的排名或位置至关重要，因为每个目标存储数据对象的不同位。具体而言，如果某个存储设备发生故障，应将其在 CRUSH 的输出列表 R 中原地替换，以使列表中的其他设备保持相同的排名（即在 R 中的位置，参见图 2）。在这种情况下，CRUSH 使用 r=r + fn 进行重新选择，其中 f 表示对 r 的失败尝试次数，从而为每个副本等级定义一个候选序列，这些候选序列在概率上不受其他副本故障的影响。相比之下，RUSH 对故障设备没有特殊处理；与其他现有的哈希分布函数一样，它隐式地假设使用“前 n 个”方法来跳过结果中的故障设备，这使得它对于奇偶校验方案来说很不方便。

3.3、地图变化和数据移动

A critical element of data distribution in a large file system is the response to the addition or removal of storage resources. CRUSH maintains a uniform distribution of data and workload at all times in order to avoid load asymmetries and the related underutilization of available resources. When an individual device fails, CRUSH flags the device but leaves it in the hierarchy, where it will be rejected and its contents uniformly redistributed by the placement algorithm (see Section 3.2.1). Such cluster map changes result in an optimal (minimum) fraction, wf ailed /W (where W is the total weight of all devices), of total data to be remapped to new storage targets because only data on the failed device is moved.

大型文件系统中数据分布的一个关键要素是对存储资源添加或移除的响应。CRUSH 始终保持数据和工作负载的均匀分布，以避免负载不对称以及由此导致的可用资源利用不足。当单个设备发生故障时，CRUSH 会标记该设备，但会将其保留在层级结构中，该设备将被拒绝，其内容将由布局算法（参见第 3.2.1 节）均匀地重新分布。此类集群映射更改会导致总数据重新映射到新存储目标的最佳（最小）比例 w /W（其中 W 是所有设备的总权重），因为只有故障设备上的数据会被移动。

The situation is more complex when the cluster hierarchy is modified, as with the addition or removal of storage resources. The CRUSH mapping process, which uses the cluster map as a weighted hierarchical decision tree, can result in additional data movement beyond the theoretical optimum of ∆w W. At each level of the hierarchy, when a shift in relative subtree weights alters the distribution, some data objects must move from from subtrees with decreased weight to those with increased weight. Because the pseudo-random placement decision at each node in the hierarchy is statistically independent, data moving into a subtree is uniformly redistributed beneath that point, and does not necessarily get remapped to the leaf item ultimately responsible for the weight change. Only at subsequent (deeper) levels of the placement process does (often different) data get shifted to maintain the correct overall relative distributions. This general effect is illustrated in the case of a binary hierarchy in Figure 3.

当集群层次结构发生修改时，情况会变得更加复杂，例如添加或删除存储资源。CRUSH 映射过程将集群映射图用作加权层次决策树，这可能会导致超出理论最优值的额外数据移动。的。在层次结构的每个级别上，当相对子树权重的变化改变了分布时，一些数据对象必须从权重降低的子树移动到权重增加的子树。由于层次结构中每个节点的伪随机放置决策在统计上是独立的，因此移动到子树的数据会在该点下方均匀地重新分布，并且不一定会重新映射到最终导致权重变化的叶项。只有在放置过程的后续（更深）级别，数据（通常不同）才会发生移动，以维持正确的整体相对分布。图 3 中的二进制层次结构说明了这种普遍效应。

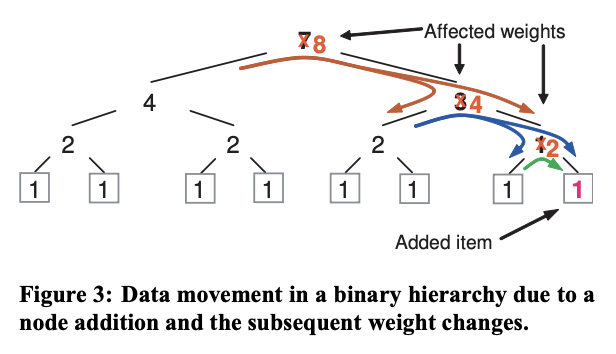
The amount of data movement in a hierarchy has a lower bound of ∆w W, the fraction of data that would reside on a newly added device with weight ∆w. Data movement increases with the height h of the hierarchy, with a conservative asymptotic upper bound of h ∆w W. The amount of movement approaches this upper bound when ∆w is small relative to W, because data objects moving into a subtree at each step of the recursion have a very low probability of being mapped to an item with a small relative weight.

层次结构中的数据移动量有一个下限，即驻留在新添加的权重为 ∆w 的设备上的数据比例。数据移动量随层次结构高度 h 的增加而增加，保守估计 h 的渐近上界。当 ∆w 相对于 W 较小时，移动量接近此上限，因为在递归的每一步中移动到子树的数据对象映射到相对权重较小的项目的概率非常低。

3.4、桶类型

Generally speaking, CRUSH is designed to reconcile two competing goals: efficiency and scalability of the mapping algorithm, and minimal data migration to restore a balanced distribution when the cluster changes due to the addition or removal of devices. To this end, CRUSH defines four different kinds of buckets to represent internal (non-leaf) nodes in the cluster hierarchy: uniform buckets, list buckets, tree buckets, and straw buckets. Each bucket type is based on a different internal data structure and utilizes a different function c(r,x) for pseudo-randomly choosing nested items during the replica placement process, representing a different tradeoff between computation and reorganization efficiency. Uniform buckets are restricted in that they must contain items that are all of the same weight (much like a conventional hash-based distribution function), while the other bucket types can contain a mix of items with any combination of weights. These differences are summarized in Table 2.

总体而言，CRUSH 的设计旨在协调两个相互竞争的目标：映射算法的效率和可扩展性，以及在集群因设备添加或移除而发生变化时，通过最小化数据迁移来恢复均衡分布。为此，CRUSH 定义了四种不同类型的 bucket 来表示集群层级结构中的内部（非叶子）节点：统一 bucket、列表 bucket、树 bucket 和秸秆 bucket。每种 bucket 类型基于不同的内部数据结构，并使用不同的函数 c(r, x) 在副本放置过程中伪随机地选择嵌套项，这代表了计算效率和重组效率之间的不同权衡。统一 bucket 的限制在于它们必须包含所有权重相同的项（非常类似于传统的基于哈希的分布函数），而其他 bucket 类型可以包含具有任意权重组合的混合项。这些差异总结如下：表 2.

3.4.1、Uniform Buckets

Devices are rarely added individually in a large system. Instead, new storage is typically deployed in blocks of identical devices, often as an additional shelf in a server rack or perhaps an entire cabinet. Devices reaching their end of life are often similarly decommissioned as a set (individual failures aside), making it natural to treat them as a unit. CRUSH uniform buckets are used to represent an identical set of devices in such circumstances. The key advantage in doing so is performance related: CRUSH can map replicas into uniform buckets in constant time. In cases where the uniformity restrictions are not appropriate, other bucket types can be used.

在大型系统中，很少单独添加设备。相反，新的存储通常以相同设备块的形式部署，通常是服务器机架中的附加机架，或者整个机柜。达到使用寿命的设备通常会以类似的方式作为一组设备退役（个别故障除外），因此将它们视为一个单元是很自然的。在这种情况下，CRUSH 统一桶用于表示一组相同的设备。这样做的主要优势在于性能：CRUSH 可以在常数时间内将副本映射到统一桶中。如果一致性限制不适用，可以使用其他类型的桶。

Given a CRUSH input value of x and a replica number r, we choose an item from a uniform bucket of size m using the function c(r,x) = (hash(x)+ rp) mod m, where p is a randomly (but deterministically) chosen prime number greater than m. For any r ≤ m we can show that we will always select a distinct item using a few simple number theory lemmas.2 For r > m this guarantee no longer holds, meaning two different replicas r with the same input x may resolve to the same item. In practice, this means nothing more than a non-zero probability of collisions and subsequent backtracking by the placement algorithm (see Section 3.2.1).

给定 CRUSH 输入值 x 和副本数量 r，我们使用函数 c(r, x) = (hash(x) + rp) mod m，从大小为 m 的均匀存储桶中选择一个项目，其中 p 是随机（但确定性地）选择的大于 m 的素数。对于任何 r ≤ m，我们可以通过一些简单的数论引理证明，我们总是会选择一个不同的项目。当 r > m 时，此保证不再成立，这意味着具有相同输入 x 的两个不同副本 r 可能解析为同一个项目。实际上，这只不过意味着碰撞概率不为零，以及随后的放置算法会进行回溯（参见第 3.2.1 节）。

If the size of a uniform bucket changes, there is a complete reshuffling of data between devices, much like conventional hash-based distribution strategies.

如果统一存储桶的大小发生变化，则设备之间的数据将完全重新排列，就像传统的基于哈希的分发策略一样。

3.4.2、List Buckets

List buckets structure their contents as a linked list, and can contain items with arbitrary weights. To place a replica, CRUSH begins at the head of the list with the most recently added item and compares its weight to the sum of all remaining items’ weights. Depending on the value of hash(x,r,item), either the current item is chosen with the appropriate probability, or the process continues recursively down the list. This approach, derived from RUSHp, recasts the placement question into that of “most recently added item, or older items?” This is a natural and intuitive choice for an expanding cluster: either an object is relocated to the newest device with some appropriate probability, or it remains on the older devices as before. The result is optimal data migration when items are added to the bucket. Items removed from the middle or tail of the list, however, can result in a significant amount of unnecessary movement, making list buckets most suitable for circumstances in which they never (or very rarely) shrink.

列表桶将其内容构建为链表，并且可以包含具有任意权重的项目。为了放置副本，CRUSH 从列表头部开始，包含最新添加的项目，并将其权重与所有剩余项目的权重之和进行比较。根据 hash(x, r, item) 的值，要么以适当的概率选择当前项目，要么该过程继续递归地沿着列表向下进行。这种方法源自 RUSHp，将放置问题重新定义为“最近添加的”问题。“是新项目，还是旧项目？”对于不断扩展的集群来说，这是一个自然而直观的选择：要么以适当的概率将对象迁移到最新的设备，要么像以前一样保留在旧设备上。当项目添加到存储桶时，其结果是最佳的数据迁移。然而，从列表中间或尾部移除项目可能会导致大量不必要的移动，因此列表存储桶最适合于从不（或很少）收缩的情况。

The RUSHp algorithm is approximately equivalent to a two-level CRUSH hierarchy consisting of a single list bucket containing many uniform buckets. Its fixed cluster representation precludes the use for placement rules or CRUSH failure domains for controlling data placement for enhanced reliability.

RUSHp 算法大致相当于一个两级 CRUSH 层次结构，由一个包含多个统一存储桶的列表存储桶组成。其固定的集群表示形式排除了使用放置规则或 CRUSH 故障域来控制数据放置以增强可靠性的可能性。

3.4.3、Tree Buckets

Like any linked list data structure, list buckets are efficient for small sets of items but may not be appropriate for large sets, where their O(n) running time may be excessive. Tree buckets, derived from RUSHt , address this problem by storing their items in a binary tree. This reduces the placement time to O(logn), making them suitable for managing much larger sets of devices or nested buckets. RUSHt is equivalent to a two-level CRUSH hierarchy consisting of a single tree bucket containing many uniform buckets.

与任何链表数据结构一样，列表桶对于较小的项目集非常高效，但对于较大的项目集可能不太适用，因为其 O(n) 运行时间可能过长。源自 RUSHt 的树形桶通过将其项目存储在二叉树中解决了这个问题。这将放置时间缩短至 O(log n)，使其适合管理更大的设备集或嵌套桶。RUSHt 相当于一个两级 CRUSH 层次结构，由一个包含多个均匀分布桶的树形桶组成。

Tree buckets are structured as a weighted binary search tree with items at the leaves. Each interior node knows the total weight of its left and right subtrees and is labeled according to a fixed strategy (described below). In order to select an item within a bucket, CRUSH starts at the root of the tree and calculates the hash of the input key x, replica number r, the bucket identifier, and the label at the current tree node (initially the root). The result is compared to the weight ratio of the left and right subtrees to decide which child node to visit next. This process is repeated until a leaf node is reached, at which point the associated item in the bucket is chosen. Only logn hashes and node comparisons are needed to locate an item.

树形存储桶的结构为带权二叉搜索树，其项目位于叶子节点。每个内部节点都知道其左右子树的总权重，并根据固定策略进行标记（详见下文）。为了在存储桶中选择一个项目，CRUSH 从树的根节点开始，计算输入键 x、副本数量 r、存储桶标识符以及当前树节点（最初为根节点）的标签的哈希值。将结果与左右子树的权重比进行比较，以决定接下来要访问哪个子节点。此过程重复进行，直到到达叶子节点，此时存储桶中的相关项目将被选中。只需进行 log n 次哈希运算和节点比较即可定位项目。

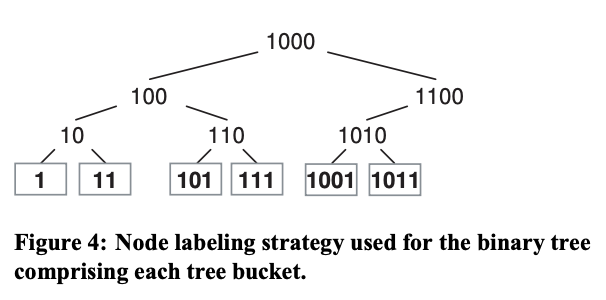
The bucket’s binary tree nodes are labeled with binary values using a simple, fixed strategy designed to avoid label changes when the tree grows or shrinks. The leftmost leaf in the tree is always labeled “1.” Each time the tree is expanded, the old root becomes the new root’s left child, and the new root node is labeled with the old root’s label shifted one bit to the left (1, 10, 100, etc.). The labels for the right side of the tree mirror those on the left side except with a “1” prepended to each value. A labeled binary tree with six leaves is shown in Figure 4. This strategy ensures that as new items are added to (or removed from) the bucket and the tree grows (or shrinks), the path taken through the binary tree for any existing leaf item only changes by adding (or removing) additional nodes at the root, at the beginning of the placement decision tree. Once an object is placed in a particular subtree, its final mapping will depend only on the weights and node labels within that subtree and will not change as long as that subtree’s items remain fixed. Although the hierarchical decision tree introduces some additional data migration between nested items, this strategy keeps movement to a reasonable level, while offering efficient mapping even for very large buckets.

存储桶的二叉树节点采用简单的固定策略标记二进制值，以避免在树增长或收缩时标签发生变化。树中最左边的叶子节点始终标记为“1”。每次树扩展时，旧根节点都会成为新根节点的左子节点，并且树中最左边的叶子节点始终带有标签，新的根节点的标签将旧根节点的标签向左移动一位（例如 1、10、100 等）。树右侧的标签与左侧的标签相同，只是每个值前面都添加了一个“1”。图 4 显示了一棵有六片叶子的带标签二叉树。此策略确保，当新项目添加到（或从）存储桶中，并且树增长（或收缩）时，任何现有叶子项目在二叉树中的路径只会通过在放置决策树的起始位置的根节点处添加（或删除）其他节点而改变。一旦对象被放置在特定的子树中，其最终映射将仅取决于该子树中的权重和节点标签，并且只要该子树的项目保持不变，映射就不会改变。尽管分层决策树在嵌套项目之间引入了一些额外的数据迁移，但此策略将移动保持在合理水平，同时即使对于非常大的存储桶也能提供高效的映射。

3.4.4、Straw Buckets

List and tree buckets are structured such that a limited number of hash values need to be calculated and compared to weights in order to select a bucket item. In doing so, they divide and conquer in a way that either gives certain items precedence (e. g., those at the beginning of a list) or obviates the need to consider entire subtrees of items at all. That improves the performance of the replica placement process, but can also introduce suboptimal reorganization behavior when the contents of a bucket change due an addition, removal, or re-weighting of an item.

列表桶和树形桶的结构使得只需计算有限数量的哈希值并将其与权重进行比较，即可选择桶中的项目。在这样做的过程中，它们会采用分治法，要么优先考虑某些项目（例如，位于列表开头的项目），要么完全无需考虑项目的整个子树。这可以提高副本放置过程的性能，但当桶的内容由于项目的添加、移除或重新调整权重而发生变化时，也可能导致重组行为不理想。

The straw bucket type allows all items to fairly “compete” against each other for replica placement through a process analogous to a draw of straws. To place a replica, a straw of random length is drawn for each item in the bucket. The item with the longest straw wins. The length of each straw is initially a value in a fixed range, based on a hash of the CRUSH input x, replica number r, and bucket item i. Each straw length is scaled by a factor f(wi) based on the item’s weight3 so that heavily weighted items are more likely to win the draw, i. e. c(r,x) = maxi(f(wi)hash(x,r,i)). Although this process is almost twice as slow (on average) than a list bucket and even slower than a tree bucket (which scales logarithmically), straw buckets result in optimal data movement between nested items when modified.

Straw 桶​​式让所有物品都能公平“竞争”。通过类似于抽签的过程，每个桶中的项目都会相互竞争以放置副本。要放置副本，需要为桶中的每个项目抽取一根随机长度的吸管。吸管最长的项目获胜。每根吸管的长度最初都是一个固定范围内的值，基于 CRUSH 输入 x、副本数量 r 和桶中项目 i 的哈希值。每根吸管的长度都会根据项目的权重乘以因子 f(w)，这样权重较大的项目更有可能获胜，即 c(r, x) = max( f(w)hash(x, r, i))。虽然此过程（平均而言）几乎比列表桶慢两倍，甚至比树桶（以对数方式缩放）更慢，但吸管桶在修改嵌套项目时可实现最佳数据移动。

The choice of bucket type can be guided based on expected cluster growth patterns to trade mapping function computation for data movement efficiency where it is appropriate to do so. When buckets are expected to be fixed (e. g., a shelf of identical disks), uniform buckets are fastest. If a bucket is only expected to expand, list buckets provide optimal data movement when new items are added at the head of the list. This allows CRUSH to divert exactly as much data to the new device as is appropriate, without any shuffle between other bucket items. The downside is O(n) mapping speed and extra data movement when older items are removed or reweighted. In circumstances where removal is expected and reorganization efficiency is critical (e. g., near the root of the storage hierarchy), straw buckets provide optimal migration behavior between subtrees. Tree buckets are an all around compromise, providing excellent performance and decent reorganization efficiency.

可以根据预期的集群增长模式来选择桶类型，在合适的情况下，以映射函数计算量换取数据移动效率。当桶预计大小固定（例如，一排相同的磁盘）时，均匀桶速度最快。如果桶预计只会扩展，则列表桶会在列表头部添加新项目时提供最佳的数据移动效果。这使得 CRUSH 能够精确地转移数据会以适当的方式迁移到新设备，而不会在其他 bucket 项之间进行任何混洗。缺点是映射速度为 O(n)，并且在移除或重新加权旧项时会产生额外的数据移动。在预期移除操作且重组效率至关重要的情况下（例如，靠近存储层次结构的根节点），straw bucket 提供了最佳的子树间迁移行为。Tree bucket 则是一种全面的折衷方案，提供了出色的性能和不错的重组效率。

4、评估

CRUSH is based on a wide variety of design goals including a balanced, weighted distribution among heterogeneous storage devices, minimal data movement due to the addition or removal of storage (including individual disk failures), improved system reliability through the separation of replicas across failure domains, and a flexible cluster description and rule system for describing available storage and distributing data. We evaluate each of these behaviors under expected CRUSH configurations relative to RUSHp and RUSHt style clusters by simulating the allocation of objects to devices and examining the resulting distribution. RUSHp and RUSHt are generalized by a two-level CRUSH hierarchy with a single list or tree bucket (respectively) containing many uniform buckets. Although RUSH’s fixed cluster representation precludes the use of placement rules or the separation of replicas across failure domains (which CRUSH uses to improve data safety), we consider its performance and data migration behavior.

CRUSH 基于多种设计目标，包括在异构存储设备之间实现均衡的加权分布，最小化由于添加或移除存储（包括单个磁盘故障）而导致的数据移动，通过跨故障域分离副本来提高系统可靠性，以及用于描述可用存储和分发数据的灵活的集群描述和规则系统。我们通过模拟对象到设备的分配并检查最终的分布情况，评估了预期 CRUSH 配置下相对于 RUSHp 和 RUSHt 风格集群的上述每一种行为。RUSHp 和 RUSHt 都由两级 CRUSH 层次结构概括，分别包含一个包含许多均匀分布的桶的列表桶和树形桶。尽管 RUSH 的固定集群表示形式排除了使用放置规则或跨故障域分离副本（CRUSH 使用这两个规则来提高数据安全性），但我们仍考虑了其性能和数据迁移行为。

4.1、数据分布

CRUSH’s data distribution should appear random uncorrelated to object identifiers x or storage targets—and result in a balanced distribution across devices with equal weight. We empirically measured the distribution of objects across devices contained in a variety of bucket types and compared the variance in device utilization to the binomial probability distribution, the theoretical behavior we would expect from a perfectly uniform random process. When distributing n objects with probability pi = wi W of placing each object on a given device i, the expected device utilization predicted by the corresponding binomial b(n, p) is µ = np with a standard deviation of σ = p np(1− p). In a large system with many devices, we can approximate 1− p ≃ 1 such that the standard deviation is σ ≃ √ µ—that is, utilizations are most even when the number of data objects is large.4 As expected, we found that the CRUSH distribution consistently matched the mean and variance of a binomial for both homogeneous clusters and clusters with mixed device weights.

CRUSH 的数据分布应该是随机的——与对象标识符 x 或存储目标无关——并最终在各设备上实现均衡的、权重相等的分布。我们根据经验测量了各种存储桶类型中对象在各设备上的分布情况，并将设备利用率的方差与二项概率分布（即我们预期的完全均匀随机过程的理论行为）进行了比较。当以 p= 的概率将 n 个对象分布到给定设备 i 上时，相应的二项式 b(n, p) 预测的预期设备利用率为 μ = np，标准差为 σ = √ np(1 − p)。在包含许多设备的大型系统中，我们可以近似 1 − p ≃ 1，使得标准差为σ ≃ μ——即当数据对象数量很大时，利用率最均匀。正如预期的那样，我们发现 CRUSH 分布对于同构集群和具有混合设备权重的集群始终与二项式的平均值和方差相匹配。

4.1.1、过载保护

Although CRUSH achieves good balancing (a low variance in device utilization) for large numbers of objects, as in any stochastic process this translates into a non-zero probability that the allocation on any particular device will be significantly larger than the mean. Unlike existing probabilistic mapping algorithms (including RUSH), CRUSH includes a per-device overload correction mechanism that can redistribute any fraction of a device’s data. This can be used to scale back a device’s allocation proportional to its overutilization when it is in danger of overfilling, selectively “leveling off” overfilled devices. When distributing data over a 1000-device cluster at 99% capacity, we found that CRUSH mapping execution times increase by less than 20% despite overload adjustments on 47% of the devices, and that the variance decreased by a factor of four (as expected).

尽管 CRUSH 能够针对大量对象实现良好的平衡（设备利用率的方差较小），但与任何随机过程一样，这意味着任何特定设备上的分配量远大于平均值的概率并非为零。与现有的概率映射算法（包括 RUSH）不同，CRUSH 包含一个针对每台设备的过载校正机制，该机制可以重新分配设备的任何部分数据。当设备面临过载风险时，该机制可用于根据设备的过度利用率按比例缩减分配量，从而有选择地“平衡”过载的设备。当在容量利用率为 99% 的 1000 台设备集群上分配数据时，我们发现，尽管对 47% 的设备进行了过载调整，但 CRUSH 映射执行时间增加的幅度不到 20%，方差也降低了四倍（符合预期）。

4.1.2、差异和部分失效

Prior research [Santos et al. 2000] has shown that randomized data distribution offers real-world system performance comparable to (but slightly slower than) that of careful data striping. In our own performance tests of CRUSH as part of a distributed object-based storage system [?], we found that randomizing object placement resulted in an approximately 5% penalty in write performance due to variance in the OSD workloads, related in turn to the level of variation in OSD utilizations. In practice, however, such variance is primarily only relevant for homogeneous workloads (usually writes) where a careful striping strategy is effective. More often, workloads are mixed and already appear random when they reach the disk (or at least uncorrelated to on-disk layout), resulting in a similar variance in device workloads and performance (despite careful layout), and similarly reduced aggregate throughput. We find that CRUSH’s lack of metadata and robust distribution in the face of any potential workload far outweigh the small performance penalty under a small set of workloads.

先前的研究 [Santos et al. 2000] 表明，随机数据分布在实际系统中的性能与谨慎的数据条带化相当（但略慢）。在我们自己对 CRUSH 作为分布式对象存储系统 [?] 的一部分进行的性能测试中，我们发现，由于 OSD 负载的差异，随机化对象放置会导致写入性能损失约 5%，这与 OSD 利用率的差异程度相关。然而，在实践中，这种差异主要只与同构负载（通常是写入）相关，在这种情况下，谨慎的条带化策略是有效的。更常见的情况是，负载是混合的，并且在到达磁盘时就已经呈现出随机性（或者至少与磁盘上的布局无关），导致设备负载和性能出现类似的差异（尽管布局谨慎），并且总吞吐量也同样降低。我们发现，CRUSH 在任何潜在负载下都缺乏元数据和稳健的分布，这远远超过了在少量负载下性能损失的益处。

This analysis assumes that device capabilities are more or less static over time. Experience with real systems suggests, however, that performance in distributed storage systems is often dragged down by a small number of slow, overloaded, fragmented, or otherwise poorly performing devices. Traditional, explicit allocation schemes can manually avoid such problem devices, while hash-like distribution functions typically cannot. CRUSH allows degenerate devices to be treated as a “partial failure” using the existing overload correction mechanism, diverting an appropriate amount of data and workload to avoiding such performance bottlenecks and correct workload imbalance over time.

此分析假设设备功能随时间变化基本保持不变。然而，实际系统经验表明，分布式存储系统的性能通常会被少数速度慢、过载、碎片化或其他性能不佳的设备拖累。传统的显式分配方案可以手动避开此类问题设备，而类似哈希的分配函数通常无法做到这一点。CRUSH 允许使用现有的过载校正机制将退化设备视为“部分故障”，从而转移适量的数据和工作负载，以避免此类性能瓶颈，并纠正随时间推移的工作负载不平衡。

Fine-grained load balancing by the storage system can further mitigate device workload variance by distributing the read workload over data replicas, as demonstrated by the DSPTF algorithm [Lumb et al. 2004]; such approaches, although complementary, fall outside the scope of the CRUSH mapping function and this paper.

存储系统进行的细粒度负载平衡可以通过在数据副本上分配读取工作负载来进一步缓解设备工作负载差异，正如 DSPTF 算法 [Lumb et al. 2004] 所证明的那样；此类方法虽然互补，但不在 CRUSH 的范围内。映射函数和本文。

4.2、重组和数据移动

We evaluate the data movement caused by the addition or removal of storage when using both CRUSH and RUSH on a cluster of 7290 devices. The CRUSH clusters are four levels deep: nine rows of nine cabinets of nine shelves of ten storage devices, for a total of 7290 devices. RUSHt and RUSHp are equivalent to a two-level CRUSH map consisting of a single tree or list bucket (respectively) containing 729 uniform buckets with 10 devices each. The results are compared to the theoretically optimal amount of movement moptimal = ∆w W , where ∆w is the combined weight of the storage devices added or removed and W is the total weight of the system. Doubling system capacity, for instance, would require exactly half of the existing data to move to new devices under an optimal reorganization.

我们评估在 7290 台设备集群上同时使用 CRUSH 和 RUSH 时，添加或移除存储所导致的数据移动。CRUSH 集群有四级深度：九排九个机柜，每排九个机架，每排十个存储设备，总共 7290 台设备。RUSHt 和 RUSHp 相当于一个两级 CRUSH 图，分别由一棵树或列表桶组成，包含 729 个均匀分布的桶，每个桶有 10 台设备。将结果与理论上的最佳移动量 moptimal = 进行比较，其中 ∆w 是添加或移除的存储设备的总权重，W 是系统的总权重。例如，将系统容量翻倍将需要根据最佳重组方案将一半的现有数据移动到新设备。

Figure 5 shows the relative reorganization efficiency in terms of the movement factor mactual/moptimal, where 1 represents an optimal number of objects moved and larger values mean additional movement. The X axis is the number of OSDs added or removed and the Y axis is the movement factor plotted on a log scale. In all cases, larger weight changes (relative to the total system) result in a more efficient reorganization. RUSHp (a single, large list bucket) dominated the extremes, with the least movement (optimal) for additions and most movement for removals (at a heavy performance penalty, see Section 4.3 below). A CRUSH multi-level hierarchy of list (for additions only) or straw buckets had the next least movement. CRUSH with tree buckets was slightly less efficient, but did almost 25% better than plain RUSHt (due to the slightly imbalanced 9-item binary trees in each tree bucket). Removals from a CRUSH hierarchy built with list buckets did poorly, as expected (see Section 3.3).

图 5 显示了以移动因子 m/m 表示的相对重组效率，其中 1 表示移动对象的最佳数量，值越大表示移动量越大。X 轴表示添加或移除的 OSD 数量，Y 轴表示以对数刻度绘制的移动因子。在所有情况下，权重变化越大（相对于整个系统而言），重组效率越高。RUSHp（单个大型列表桶）在极端情况下表现最佳，添加操作的移动量最少（最优），而移除操作的移动量最多（性能损失严重，参见下文 4.3 节）。CRUSH 多级层级结构（仅用于添加操作）或 Straw 桶的移动量次之。使用树形桶的 CRUSH 效率略低，但比普通 RUSHt 的性能高出近 25%（原因是每个树形桶中的 9 项二叉树略微不平衡）。使用列表桶构建的 CRUSH 层级结构的移除操作性能不佳，正如预期的那样（参见 3.3 节）。

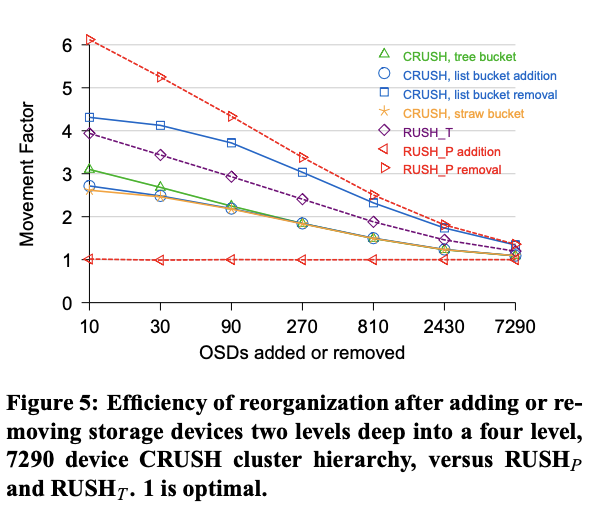
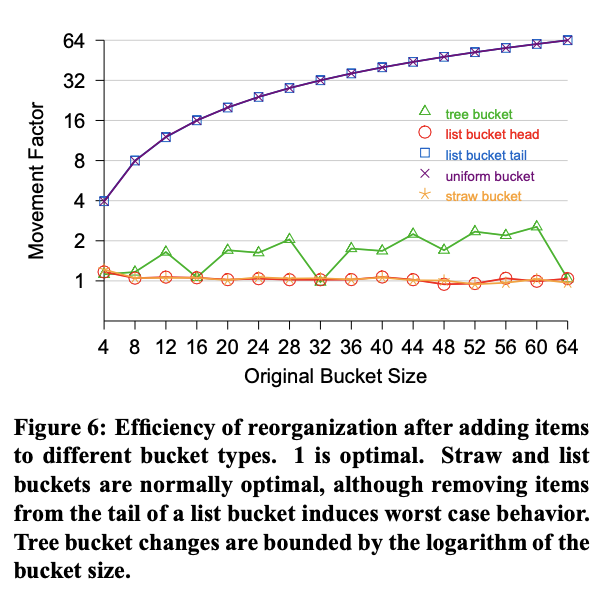
Figure 6 shows the reorganization efficiency of different bucket types (in isolation) when nested items are added or removed. The movement factor in a modified tree bucket is bounded by logn, the depth of its binary tree. Adding items to straw and list buckets is approximately optimal. Uniform bucket modifications result in a total reshuffle of data. Modifications to the tail of a list (e. g., removal of the oldest storage) similarly induce data movement proportional to the bucket size. Despite certain limitations, list buckets may be appropriate in places within an overall storage hierarchy where removals are rare and at a scale where the performance impact will be minimal. A hybrid approach combining uniform, list, tree, and straw buckets can minimize data movement under the most common reorganization scenarios while still maintaining good mapping performance.

图 6 展示了当添加或删除嵌套项时，不同 bucket 类型（单独）的重组效率已移除。修改后的树形桶中的移动因子受其二叉树深度 log n 的限制。向秸秆桶和列表桶中添加项目近似为最优选择。均匀桶的修改会导致数据的彻底重组。修改列表的尾部（例如，移除最旧的存储）同样会引起与桶大小成比例的数据移动。尽管存在某些限制，但列表桶可能适用于整体存储层次结构中很少发生移除操作且性能影响最小的地方。结合均匀桶、列表桶、树形桶和秸秆桶的混合方法可以在最常见的重组场景下最大限度地减少数据移动，同时仍保持良好的映射性能。

4.3、算法性能

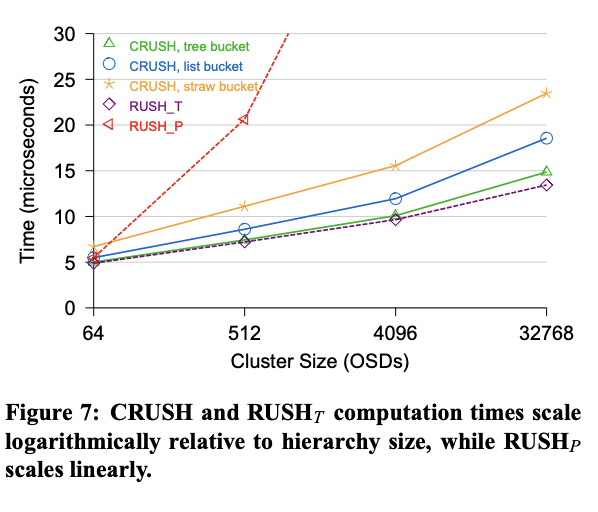
Calculating a CRUSH mapping is designed to be fast O(logn) for a cluster with n OSDs—so that devices can quickly locate any object or reevaluate the proper storage targets for the objects that they already store after a cluster map change. We examine CRUSH’s performance relative to RUSHp and RUSHt over a million mappings into clusters of different sizes. Figure 7 shows the average time (in microseconds) to map a set of replicas into a CRUSH cluster composed entirely of 8-item tree and uniform buckets (the depth of the hierarchy is varied) versus RUSH’s fixed twolevel hierarchy. The X axis is the number of devices in the system, and is plotted on a log scale such that it corresponds to the depth of the storage hierarchy. CRUSH performance is logarithmic with respect to the number of devices. RUSHt edges out CRUSH with tree buckets due to slightly simpler code complexity, followed closely by list and straw buckets. RUSHp scales linearly in this test (taking more than 25 times longer than CRUSH for 32768 devices), although in practical situations where the size of newly deployed disks increases exponentially over time one can expect slightly improved sub-linear scaling [Honicky and Miller 2004]. These tests were conducted with a 2.8 GHz Pentium 4, with overall mapping times in the tens of microseconds.

CRUSH 映射的计算速度被设计得非常快——对于包含 n 个 OSD 的集群，其复杂度为 O(log n)——这样设备就可以快速定位任何对象，或者在集群映射更改后重新评估已存储对象的正确存储目标。我们比较了 CRUSH 与 RUSHp/RUSHt 的性能，对比了超过一百万次映射到不同规模集群的映射。图 7 显示了将一组副本映射到完全由 8 项树形和均匀存储桶（层级深度可变）组成的 CRUSH 集群的平均时间（以微秒为单位），以及 RUSH 固定的两级层级结构。X 轴表示系统中的设备数量，并以对数刻度绘制，使其与存储层级的深度相对应。CRUSH 的性能与设备数量呈对数关系。由于代码复杂度略低，RUSHt 凭借树形存储桶的优势略胜一筹，其次是 list 和 straw 存储桶。RUSHp 在本测试中呈线性增长（耗时超过 25 。对于 32768 个设备，这比 CRUSH 要长 1 倍（虽然在实际情况下，新部署的磁盘大小会随时间呈指数增长，但可以预期亚线性扩展会略有改善 [Honicky and Miller 2004]）。这些测试是在 2.8 GHz Pentium 4 上进行的，总体映射时间在几十微秒内。

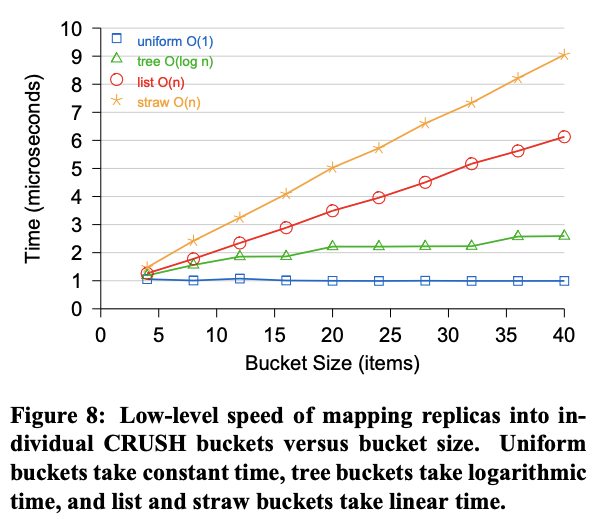
The efficiency of CRUSH depends upon the depth of the storage hierarchy and on the types of buckets from which it is built. Figure 8 compares the time (Y) required for c(r,x) to select a single replica from each bucket type as a function of the size of the bucket (X). At a high level, CRUSH scales as O(logn)—linearly with the hierarchy depth—provided individual buckets that may be O(n) (list and straw buckets scale linearly) do not exceed a fixed maximum size. When and where individual bucket types should be used depends on the expected number of additions, removals, or re-weightings. List buckets offer a slight performance advantage over straw buckets, although when removals are possible one can expect excessive data shuffling. Tree buckets are a good choice for very large or commonly modified buckets, with decent computation and reorganization costs.

CRUSH 的效率取决于存储层级的深度以及构建它的桶的类型。图 8 比较了 c(r, x) 从每种桶类型中选择单个副本所需的时间 (Y) 与桶大小 (X) 的关系。从高层次来看，CRUSH 的扩展速度为 O(log n)——与层级深度呈线性关系——前提是单个桶（可能是 O(n) 的桶，列表桶和 Straw 桶呈线性扩展）不超过固定的最大大小。何时何地使用单个桶类型取决于预期的添加、删除或重新加权次数。列表桶的性能略优于 Straw 桶，但当可以进行删除操作时，可以进一步避免过度的数据混排。对于非常大或经常修改的桶，树形桶是一个不错的选择，具有合理的计算和重组成本。

Central to CRUSH’s performance—both the execution time and the quality of the results—is the integer hash function used. Pseudo-random values are calculated using a multiple input integer hash function based on Jenkin’s 32-bit hash mix [Jenkins 1997]. In its present form, approximately 45% of the time spent in the CRUSH mapping function is spent hashing values, making the hash key to both overall speed and distribution quality and a ripe target for optimization.

CRUSH 性能（包括执行时间和结果质量）的核心在于其所使用的整数哈希函数。伪随机值是使用基于 Jenkin 32 位哈希混合算法的多输入整数哈希函数计算得出的 [Jenkins 1997]。目前，CRUSH 映射函数中大约 45% 的时间用于哈希值计算，这使得哈希值成为整体速度和分发质量的关键，也是优化的成熟目标。

4.3.1、疏忽老龄化

CRUSH leaves failed devices in place in the storage hierarchy both because failure is typically a temporary condition (failed disks are usually replaced) and because it avoids inefficient data reorganization. If a storage system ages in neglect, the number of devices that are failed but not replaced may become significant. Although CRUSH will redistribute data to non-failed devices, it does so at a small performance penalty due to a higher probability of backtracking in the placement algorithm. We evaluated the mapping speed for a 1,000 device cluster while varying the percentage of devices marked as failed. For the relatively extreme failure scenario in which half of all devices are dead, the mapping calculation time increases by 71%. (Such a situation would likely be overshadowed by heavily degraded I/O performance as each devices’ workload doubles.)

CRUSH 将故障设备保留在存储层级结构中，一方面是因为故障通常只是暂时现象（故障磁盘通常会被替换），另一方面是因为它避免了低效的数据重组。如果存储系统老化且无人照管，发生故障但未被替换的设备数量可能会变得非常庞大。虽然 CRUSH 会将数据重新分配到未发生故障的设备上，但由于布局算法中回溯的概率较高，因此会略微降低性能。我们评估了一个包含 1,000 个设备的集群的映射速度，同时改变了标记为故障的设备百分比。在相对极端的故障场景下，即一半设备都已失效，映射计算时间会增加 71%。（这种情况可能会被 I/O 性能的严重下降所掩盖，因为每个设备的工作负载都会翻倍。）

4.4、可靠性

Data safety is of critical importance in large storage systems, where the large number of devices makes hardware failure the rule rather than the exception. Randomized distribution strategies like CRUSH that decluster replication are of particular interest because they expand the number of peers with which any given device shares data. This has two competing and (generally speaking) opposing effects. First, recovery after a failure can proceed in parallel because smaller bits of replicated data are spread across a larger set of peers, reducing recovery times and shrinking the window of vulnerability to additional failures. Second, a larger peer group means an increased probability of a coincident second failure losing shared data. With 2-way mirroring these two factors cancel each other out, while overall data safety with more than two replicas increases with declustering [Xin et al. 2004].

在大型存储系统中，数据安全至关重要。由于设备数量众多，硬件故障成为常态而非例外。像 CRUSH 这样能够去集群复制的随机分布策略尤其值得关注，因为它们可以扩展任何给定设备与其共享数据的对等节点数量。这会产生两种相互竞争且（一般而言）相反的效果。首先，故障后的恢复可以并行进行，因为较小的复制数据位分散在更大的对等节点集合中，从而缩短了恢复时间并缩小了对其他故障的脆弱性窗口。其次，更大的对等节点组意味着同时发生第二次故障并丢失共享数据的概率增加。在双向镜像中，这两个因素相互抵消，而使用去集群技术，拥有两个以上副本的整体数据安全性会提高 [Xin et al. 2004]。

However, a critical issue with multiple failures is that, in general, one cannot expect them to be independent—in many cases a single event like a power failure or a physical disturbance will affect multiple devices, and the larger peer groups associated with declustered replication greatly increase the risk of data loss. CRUSH’s separation of replicas across user-defined failure domains (which does not exist with RUSH or existing hash-based schemes) is specifi cally designed to prevent concurrent, correlated failuresfrom causing data loss. Although it is clear that the risk is reduced, it is difficult to quantify the magnitude of the improvement in overall system reliability in the absence of a specific storage cluster configuration and associated historical failure data to study. Although we hope to perform such a study in the future, it is beyond the scope of this paper.

然而，多重故障的一个关键问题是，一般来说，人们不能指望它们是独立的——在许多情况下，像电源故障或物理干扰这样的单一事件就会影响多个设备，而与非集群复制相关的更大的对等组会大大增加数据丢失的风险 CRUSH 将副本分离到用户定义的故障域（RUSH 或现有的基于哈希的方案均不存在此功能），其设计初衷是防止并发关联故障导致数据丢失。虽然风险明显降低，但在缺乏特定存储集群配置和相关历史故障数据可供研究的情况下，很难量化整体系统可靠性的提升幅度。虽然我们希望在未来开展此类研究，但这超出了本文的讨论范围。

5、未来工作

CRUSH is being developed as part of Ceph, a multi-petabyte distributed file system [?]. Current research includes an intelligent and reliable distributed object store based largely on the unique features of CRUSH. The primitive rule structure currently used by CRUSH is just complex enough to support the data distribution policies we currently envision. Some systems will have specific needs that can be met with a more powerful rule structure.

CRUSH 是 Ceph（一个多 PB 级分布式文件系统 [?]）的一部分，目前正在开发中。目前的研究包括一个智能可靠的分布式对象存储，主要基于 CRUSH 的独特功能。CRUSH 目前使用的原始规则结构复杂度刚好足以支持我们目前设想的数据分布策略。某些系统会有特定的需求，可以通过更强大的规则结构来满足。

Although data safety concerns related to coincident failures were the primary motivation for designing CRUSH, study of real system failures is needed to determine their character and frequency before Markov or other quantitative models can used to evaluate their precise effect on a system’s mean time to data loss (MTTDL).

尽管与同时发生的故障相关的数据安全问题是设计 CRUSH 的主要动机，但在使用马尔可夫或其他定量模型来评估它们对系统平均数据丢失时间 (MTTDL) 的精确影响之前，需要研究真实的系统故障以确定其特征和频率。

CRUSH’s performance is highly dependent on a suitably strong multi-input integer hash function. Because it simultaneously affects both algorithmic correctness—the quality of the resulting distribution—and speed, investigation into faster hashing techniques that are sufficiently strong for CRUSH is warranted.

CRUSH 的性能高度依赖于足够强大的多输入整数哈希函数。由于它同时影响算法的正确性（最终分布的质量）和速度，因此有必要研究能够满足 CRUSH 要求的更快、更强大的哈希技术。

6、结论

Distributed storage systems present a distinct set of scalability challenges for data placement. CRUSH meets these challenges by casting data placement as a pseudo-random mapping function, eliminating the conventional need for allocation metadata and instead distributing data based on a weighted hierarchy describing available storage. The structure of the cluster map hierarchy can reflect the underlying physical organization and infrastructure of an installation, such as the composition of storage devices into shelves, cabinets, and rows in a data center, enabling custom placement rules that define a broad class of policies to separate object replicas into different user-defined failure domains (with, say, independent power and network infrastructure). In doing so, CRUSH can mitigate the vulnerability to correlated device failures typical of existing pseudo-random systems with declustered replication. CRUSH also addresses the risk of device overfilling inherent in stochastic approaches by selectively diverting data from overfilled devices, with minimal computational cost.

分布式存储系统在数据放置方面面临着一系列独特的可扩展性挑战。CRUSH 通过将数据放置转换为伪随机映射函数来应对这些挑战，消除了对分配元数据的传统需求，而是基于描述可用存储空间的加权层次结构来分配数据。集群映射层次结构可以反映设施的底层物理组织和基础架构，例如数据中心中存储设备在机架、机柜和行中的组成，从而支持自定义放置规则，这些规则定义了一系列广泛的策略，将对象副本划分到不同的用户自定义故障域（例如，具有独立电源和网络基础架构）。通过这样做，CRUSH 可以缓解现有采用非集群复制的伪随机系统通常存在的关联设备故障问题。CRUSH 还通过选择性地从过载设备中转移数据，以最小的计算成本解决了随机方法固有的设备过载风险。

CRUSH accomplishes all of this in an exceedingly efficient fashion, both in terms of the computational efficiency and the required metadata. Mapping calculations have O(logn) running time, requiring only tens of microseconds to execute with thousands of devices. This robust combination of efficiency, reliability and flexibility makes CRUSH an appealing choice for large-scale distributed storage systems.

CRUSH 以极其高效的方式完成了所有这些工作，无论是在计算效率方面
效率和所需的元数据。映射计算的运行时间为 O(log n)，在数千台设备上执行仅需数十微秒。这种高效、可靠和灵活的强强联合，使 CRUSH 成为大规模分布式存储系统的理想之选。

7、致谢

R. J. Honicky’s excellent work on RUSH inspired the development of CRUSH. Discussions with Richard Golding, Theodore Wong, and the students and faculty of the Storage Systems Research Center were most helpful in motivating and refining the algorithm. This work was supported in part by Lawrence Livermore National Laboratory, Los Alamos National Laboratory, and Sandia National Laboratory under contract B520714. Sage Weil was supported in part by a fellowship from Lawrence Livermore National Laboratory. We would also like to thank the industrial sponsors of the SSRC, including Hewlett Packard Laboratories, IBM, Intel, Microsoft Research, Network Appliance, Onstor, Rocksoft, Symantec, and Yahoo.

RJ Honicky 在 RUSH 上的出色工作启发了 CRUSH 的开发。与 Richard Golding、Theodore Wong 以及存储系统研究中心 (SSRC) 的学生和教员的讨论对算法的启发和改进起到了至关重要的作用。这项工作得到了劳伦斯利弗莫尔国家实验室、洛斯阿拉莫斯国家实验室和桑迪亚国家实验室的部分支持，合同编号为 B520714。Sage Weil 的部分研究得到了劳伦斯利弗莫尔国家实验室的奖学金资助。我们还要感谢 SSRC 的行业赞助商，包括惠普实验室、IBM、英特尔、微软研究院、Network Appliance、Onstor、Rocksoft、赛门铁克和雅虎。

8、可用性

The CRUSH source code is licensed under the LGPL, and is available at: http://www.cs.ucsc.edu/~sage/crush

CRUSH 源代码采用 LGPL 许可，可从以下位置获取：http://www.cs.ucsc.edu/~sage/crush

参考

[1] ANDERSON, E., HALL, J., HARTLINE, J., HOBBS, M., KARLIN, A. R., SAIA, J., SWAMINATHAN, R., AND WILKES, J. 2001. An experimental study of data migration algorithms. In Proceedings of the 5th International Workshop on Algorithm Engineering, SpringerVerlag, London, UK, 145–158.
ANDERSON, E., HOBBS, M., KEETON, K., SPENCE, S., UYSAL, M., AND VEITCH, A. 2002. Hippodrome: running circles around storage administration. In Proceedings of the 2002 Conference on File and Storage Technologies (FAST).
[2] AZAGURY, A., DREIZIN, V., FACTOR, M., HENIS, E., NAOR, D., RINETZKY, N., RODEH, O., SATRAN, J., TAVORY, A., AND YERUSHALMI, L. 2003. Towards an object store. In Proceedings of the 20th IEEE / 11th NASA Goddard Conference on Mass Storage Systems and Technologies, 165–176.
[3] BRAAM, P. J. 2004. The Lustre storage architecture. http://www.lustre.org/documentation.html, Cluster File Systems, Inc., Aug.
[4] BRINKMANN, A., SALZWEDEL, K., AND SCHEIDELER, C. 2000. Efficient, distributed data placement strategies for storage area networks. In Proceedings of the 12th ACM Symposium on Parallel Algorithms and Architectures (SPAA), ACM Press, 119–128. Extended Abstract.
[5] CHOY, D. M., FAGIN, R., AND STOCKMEYER, L. 1996. Efficiently extendible mappings for balanced data distribution. Algorithmica 16, 215–232.
[6] GHEMAWAT, S., GOBIOFF, H., AND LEUNG, S.-T. 2003. The Google file system. In Proceedings of the 19th ACM Symposium on Operating Systems Principles (SOSP ‘03), ACM.
[7] GOBIOFF, H., GIBSON, G., AND TYGAR, D. 1997. Security for network attached storage devices. Tech. Rep. TR CMU-CS-97-185, Carniege Mellon, Oct.
[8] GOEL, A., SHAHABI, C., YAO, D. S.-Y., AND ZIMMERMAN, R. 2002. SCADDAR: An efficient randomized technique to reorganize continuous media blocks. In Proceedings of the 18th International Conference on Data Engineering (ICDE ‘02), 473–482.
[9] GRANVILLE, A. 1993. On elementary proofs of the Prime Number Theorem for Arithmetic Progressions, without characters. In Proceedings of the 1993 Amalfi Conference on Analytic Number Theory, 157–194.
[10] HONICKY, R. J., AND MILLER, E. L. 2004. Replication under scalable hashing: A family of algorithms for scalable decentralized data distribution. In Proceedings of the 18th International Parallel & Distributed Processing Symposium (IPDPS 2004), IEEE.
[11] JENKINS, R. J., 1997. Hash functions for hash table lookup. http://burtleburtle.net/bob/hash/evahash.html.
[12] KARGER, D., LEHMAN, E., LEIGHTON, T., LEVINE, M., LEWIN, D., AND PANIGRAHY, R. 1997. Consistent hashing and random trees: Distributed caching protocols for relieving hot spots on the World Wide Web. In ACM Symposium on Theory of Computing, 654–663.
[13] LUMB, C. R., GANGER, G. R., AND GOLDING, R. 2004. D-SPTF: Decentralized request distribution in brick-based storage systems. In Proceedings of the 11th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS), 37–47.
[14] NAGLE, D., SERENYI, D., AND MATTHEWS, A. 2004. The Panasas ActiveScale storage cluster—delivering scalable high bandwidth storage. In Proceedings of the 2004 ACM/IEEE Conference on Supercomputing (SC ‘04).
[15] RODEH, O., AND TEPERMAN, A. 2003. zFS—a scalable distributed file system using object disks. In Proceedings of the 20th IEEE / 11th NASA Goddard Conference on Mass Storage Systems and Technologies, 207–218.
[16] SAITO, Y., FRØLUND, S., VEITCH, A., MERCHANT, A., AND SPENCE, S. 2004. FAB: Building distributed enterprise disk arrays from commodity components. In Proceedings of the 11th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS), 48–58.
[17] SANTOS, J. R., MUNTZ, R. R., AND RIBEIRO-NETO, B. 2000. Comparing random data allocation and data striping in multimedia servers. In Proceedings of the 2000 SIGMETRICS Conference on Measurement and Modeling of Computer Systems, ACM Press, Santa Clara, CA, 44–55.
[18] SCHMUCK, F., AND HASKIN, R. 2002. GPFS: A shareddisk file system for large computing clusters. In Proceedings of the 2002 Conference on File and Storage Technologies (FAST), USENIX, 231–244.
[19] TANG, H., GULBEDEN, A., ZHOU, J., STRATHEARN, W., YANG, T., AND CHU, L. 2004. A self-organizing storage cluster for parallel data-intensive applications. In Proceedings of the 2004 ACM/IEEE Conference on Supercomputing (SC ‘04).
[20] XIN, Q., MILLER, E. L., AND SCHWARZ, T. J. E. 2004. Evaluation of distributed recovery in large-scale storage systems. In Proceedings of the 13th IEEE International Symposium on High Performance Distributed Computing (HPDC), 172–181