译作: 可扩展哈希下的复制: 可扩展分散数据分布的算法家族 , 原文地址，该论文发表于 2004 年 4 月在新墨西哥州圣达菲举行的第 18 届国际并行和分布式处理研讨会 (IPDPS 2004) 论文集。这篇论文介绍了一系列名为 RUSH(Replication Under Scalable Hashing) 的算法，用于在去中心化的存储系统中分配和管理数据。每种 RUSH 变体都有其独特的优势和局限性，选择哪一种取决于具体的系统需求和操作环境。

算法特点:

允许在线调整特定对象的复制程度，且不受其他对象复制程度的影响。
保证数据复制的安全性，即确保同一对象的副本不会存储在同一硬盘上。
支持加权，允许将不同年份的磁盘添加到系统中。加权可以让系统充分利用最新的技术，也可以淘汰较旧的技术。
支持最佳或接近最佳的重组，当系统添加/淘汰磁盘时，会最大限度地减少需要移动的对象数量，以使系统恢复平衡。
支持在线重组，无需长时间锁定文件系统。
完全去中心化，无需中央目录，客户端可以并行计算数据位置。
极少的资源需求，算法速度非常快，并且占用的内存极少。

算法类别:

RUSHp ：Replication Under Scalable Hashing using Primes
- 特点:
  - 使用素数和参数哈希技术进行数据放置
  - 支持在线调整复制因子，允许动态调整特定对象的复制数量
  - 允许除原始子集群之外的所有子集群的磁盘数量都少于对象副本因子
  - 适用于添加新服务器时的数据重新分配，但不适合移除服务器
- 适用场景:
  - 小型到中型存储系统，特别是在存储空间宝贵且需要数据保护（如纠删码）的环境中
  - 系统扩展时主要通过添加新的存储单元
- 优点:
  - 支持纠删码，适合存储空间有限的环境
  - 在添加存储单元时能有效地重新分配数据，减少数据迁移
- 缺点:
  - 不支持存储单元的移除，移除存储单元时可能需要显著的数据重组
  - 需要保证系统中的每个子集群至少有与对象副本数相等的磁盘数量
RUSHr : Replication Under Scalable Hashing with Removal support
- 特点:
  - 设计用于支持存储单元的动态添加和移除
  - 使用超几何分布来决定对象在各个子集群中的分布
  - 在重组时尝试最小化移动的数据量
- 适用场景:
  - 需要频繁进行存储单元添加或移除的大型存储系统
  - 系统在运行中可能需要调整存储单元的权重或进行其他形式的在线重组
- 优点:
  - 支持存储单元的动态添加和移除，提供极大的配置灵活性
  - 在存储单元权重调整和系统重组时表现良好
- 缺点:
  - 在大规模系统中，查找性能可能不如RUSHt，尤其是在频繁重组的环境下
RUSHt : Replication Under Scalable Hashing using Trees
- 特点:
  - 使用二叉树结构优化查找性能，使查找时间与子集群数量呈对数关系
  - 支持复杂的重组操作，如整体子集群的添加和移除
  - 提供最优或接近最优的数据重组行为
- 适用场景:
  - 非常大的存储系统，需要高性能和高并行性
  - 系统规模大，且可能需要频繁地进行大规模的重组
- 优点:
  - 查找性能优异，特别是在系统经过多次重组后
  - 在多种重组场景下提供最佳或接近最佳的行为
- 缺点:
  - 每个子集群必须至少有与对象最大副本数相等的磁盘数量，这可能限制了小规模系统的使用
  - 在处理单个磁盘的移除时可能需要额外的机制来减少影响

摘要

Typical algorithms for decentralized data distribution work best in a system that is fully built before it first used; adding or removing components results in either extensive reorganization of data or load imbalance in the system. We have developed a family of decentralized algorithms, RUSH (Replication Under Scalable Hashing), that maps replicated objects to a scalable collection of storage servers or disks. RUSH algorithms distribute objects to servers according to user-specified server weighting. While all RUSH variants support addition of servers to the system, different variants have different characteristics with respect to lookup time in petabyte-scale systems, performance with mirroring (as opposed to redundancy codes), and storage server removal. All RUSH variants redistribute as few objects as possible when new servers are added or existing servers are removed, and all variants guarantee that no two replicas of a particular object are ever placed on the same server. Because there is no central directory, clients can compute data locations in parallel, allowing thousands of clients to access objects on thousands of servers simultaneously.

典型的去中心化数据分布算法在首次使用前就已完全构建的系统中效果最佳；添加或删除组件会导致数据大规模重组或系统负载不平衡。我们开发了一系列去中心化算法，RUSH（可扩展哈希下的复制），它将复制的对象映射到可扩展的存储服务器或磁盘集合。RUSH 算法根据用户指定的服务器权重将对象分发到服务器。虽然所有 RUSH 变体都支持向系统添加服务器，但不同变体在 PB 级系统中的查找时间、镜像（而非冗余代码）的性能以及存储服务器移除方面具有不同的特性。所有 RUSH 变体在添加新服务器或移除现有服务器时都会重新分配尽可能少的对象，并且所有变体都保证同一对象的两个副本永远不会被放置在同一服务器上。由于没有中央目录，客户端可以并行计算数据位置，从而允许数千个客户端同时访问数千台服务器上的对象。

1、介绍

Recently, there has been significant interest in using object-based storage as a mechanism for increasing the scalability of storage systems. The storage industry has begun to develop standard protocols and models for object based storage [19], and various other major players in the industry, such as the National Laboratories have also pushed for the development of object-based storage devices (OSDs) to meet their growing demand for storage bandwidth and scalability. The OSD architecture differs from a typical storage area network (SAN) architecture in that block management is handled by the disk as opposed to a dedicated server. Because block management on individual disks requires no inter-disk communication, this redistribution of work comes at little cost in performance or efficiency, and has a huge benefit in scalability, since block layout is completely parallelized.

近年来，人们对使用基于对象的存储作为提高存储系统可扩展性的机制产生了浓厚的兴趣。存储行业已经开始开发基于对象的存储的标准协议和模型[19]，行业中的其他主要参与者，例如国家实验室，也在推动基于对象的存储设备（OSD）的开发，以满足其对存储带宽和可扩展性日益增长的需求。OSD 架构与典型的存储区域网络 (SAN) 架构不同，其块管理由磁盘而非专用服务器负责。由于单个磁盘上的块管理无需磁盘间通信，因此这种工作重新分配几乎不会影响性能或效率，而且由于块布局完全并行化，因此在可扩展性方面具有巨大优势。

There are differing opinions about what object-based storage is or should be, and how much intelligence belongs in the disk. In order for a device to be an OSD, however, each disk or disk subsystem must have its own filesystem; an OSD manages its own allocation of blocks and disk layout. To store data on an OSD, a client provides the data and a key for the data. To retrieve the data, a client provides a key. In this way, an OSD has many similarities to an object database.

关于对象存储是什么或应该是什么，以及磁盘应具备多少智能，存在着不同的观点。然而，要使设备成为 OSD，每个磁盘或磁盘子系统必须拥有自己的文件系统；OSD 管理其自身的块分配和磁盘布局。要在 OSD 上存储数据，客户端需要提供数据和数据的密钥。要检索数据，客户端需要提供密钥。因此，OSD 与对象数据库有很多相似之处。

Large storage systems built from individual OSDs still have a scalability problem, however: where should individual objects be placed? We have developed a family of algorithms, RUSH (Replication Under Scalable Hashing) that addresses this problem by facilitating the distribution of multiple replicas of objects among thousands of OSDs. RUSH allows individual clients to compute the location of all of the replicas of a particular object in the system algorithmically using just a list of storage servers rather than relying on a directory. Equally important, a simple algorithm for the lookup and placement of data to a function from a key to a particular OSD makes it easy to support complex management functionality such as weighting for disk clusters with different characteristics and online reorganization.

然而，由单个 OSD 构建的大型存储系统仍然存在可扩展性问题: 单个对象应该放在哪里？我们开发了一系列算法，RUSH（可扩展哈希下的复制），通过在数千个 OSD 之间分配对象的多个副本来解决此问题。RUSH 允许单个客户端仅使用存储服务器列表（而非依赖目录）以算法方式计算系统中特定对象所有副本的位置。同样重要的是，一个简单的算法，用于从键到特定 OSD 的函数查找和放置数据，可以轻松支持复杂的管理功能，例如为具有不同特性的磁盘集群分配权重以及在线重组。

2. RUSH 算法家族

One important aspect of large scalable storage systems is replication. Qin, et al. [21] note that, without replication or another form of data protection such as erasure coding, a two petabyte storage system would have a mean time to data loss of around one day. It is therefore important that an object placement algorithm support replication or another method of data protection.

大型可扩展存储系统的一个重要方面是复制。Qin 等人 [21] 指出，如果没有复制或其他形式的数据保护（例如擦除编码），一个 2PB 的存储系统平均需要大约一天的数据丢失。因此，对象放置算法支持复制或其他数据保护方法非常重要。

Since our algorithms all support replication and other features necessary for truly scalable OSD-based storage systems, we have named the family of algorithms which we have developed, Replication Under Scalable Hashing, or RUSH. In fact, RUSH variants support something stronger: adjustable replication. That is, RUSH variants allow the degree of replication of a particular object to be adjusted online, independent of the degree of replication of other objects. Adjustable replication can be used to significantly increase the mean time to data loss in an OSD based system [21].

由于我们的算法都支持复制以及其他真正可扩展的基于 OSD 的存储系统所需的功能，我们将开发的算法系列命名为”可扩展哈希下的复制”（Replication Under Scalable Hashing），简称 RUSH。事实上，RUSH 的变体支持更强大的功能: 可调复制。也就是说，RUSH 变体允许在线调整特定对象的复制程度，且不受其他对象复制程度的影响。可调复制可以显著提高基于 OSD 的系统的平均数据丢失时间[21]。

It is also important to note that in order for replication to be effective, it must guarantee that replicas of the same objects are placed on different disks. While some peer-to-peer systems such as OceanStore [15] do not make such guarantees, but rather use high degrees of replication to make statistical promises about the number of independent replicas, RUSH variants all make this guarantee. RUSH variants also distribute the replicas of the objects stored on a particular disk throughout the system, so that all of the disks in the system share the burden of servicing requests from a failed disk.

还需要注意的是，为了使复制有效，必须保证相同对象的副本位于不同的磁盘上。虽然某些对等系统（例如 OceanStore [15]）并未提供此类保证，而是使用高副本数来统计独立副本的数量，但 RUSH 的变体均能提供此类保证。RUSH 的变体还会将存储在特定磁盘上的对象的副本分布到整个系统中，以便系统中的所有磁盘分担处理故障磁盘请求的负担。

Since many storage systems are upgraded and expanded periodically, RUSH variants also support weighting, allowing disks of different vintages to be added to a system. Weighting allows a system to take advantage of the newest technology, and can also allow older technology to be retired.

由于许多存储系统会定期升级和扩展，RUSH 的变体也支持加权，允许将不同年份的磁盘添加到系统中。加权可以让系统充分利用最新的技术，也可以淘汰较旧的技术。

Another essential characteristic of RUSH variants is optimal or near-optimal reorganization. When new disks are added to the system, or old disks are retired, RUSH variants minimize the number of objects that need to be moved in order to bring the system back into balance. This is in sharp contrast to pseudo-random placement using a traditional hash function, under which most objects need to be moved in order to bring a system back into balance. Additionally, RUSH variants can perform reorganization online without locking the filesystem for a long time to relocate data. Near-optimal reorganization is important because completely reorganizing a very large filesystem is very slow, and may take a filesystem offline for many hours. For example, a 1 petabyte file system built from 2000 disks, each with a 500 GB capacity and peak transfer rate of 25 MB/sec would require nearly 12 hours to shuffle all of the data; this would require an aggregate network bandwidth of 50 GB/s. During reorganization, the system would be unavailable. In contrast, a system running RUSH can reorganize online because only a small fraction of existing disk bandwidth is needed to copy data to the new disks.

RUSH 变体的另一个重要特性是最佳或接近最佳的重组。当系统添加新磁盘或淘汰旧磁盘时，RUSH 变体会最大限度地减少需要移动的对象数量，以使系统恢复平衡。这与使用传统哈希函数的伪随机布局形成了鲜明对比，在伪随机布局下，大多数对象都需要移动才能使系统恢复平衡。此外，RUSH 变体可以在线执行重组，而无需长时间锁定文件系统来重新定位数据。接近最佳的重组非常重要，因为完全重组一个非常大的文件系统非常慢，并且可能导致文件系统离线数小时。例如，一个由 2000 个磁盘构建的 1PB 文件系统，每个磁盘的容量为 500GB，峰值传输速率为 25MB/秒，需要近 12 小时才能完成所有数据的 shuffle；这将需要 50GB/秒的总网络带宽。在重组期间，系统将不可用。相比之下，运行 RUSH 的系统可以在线重组，因为只需要一小部分现有磁盘带宽即可将数据复制到新磁盘。

RUSH variants are completely decentralized, so they require no communication except during a reorganization. As a storage system scales to tens or even hundreds of thousands of disks, decentralization of object lookup becomes more and more essential. Moreover,RUSH variants require very few resources to run effectively: RUSH variants are very fast and require minimal memory. These two features enable the algorithms to be run not only on the clients, but on the OSDs themselves, even under severely constrained memory and processing requirements. Running on the OSD can assist in fast failure recovery.

RUSH 变体完全去中心化，因此除了重组期间外，无需任何通信。随着存储系统扩展到数万甚至数十万个磁盘，对象查找的去中心化变得越来越重要。此外，RUSH 变体只需极少的资源即可有效运行: RUSH 变体速度非常快，并且占用的内存极少。这两个特性使得算法不仅可以在客户端上运行，还可以在 OSD 上运行，即使在内存和处理能力严重受限的情况下也是如此。在 OSD 上运行有助于快速故障恢复。

2.1、术语和符号

RUSH variants are able to offer such flexibility and performance in part because they make assumptions about the structure of the OSDs and clients. First, we assume that disks and clients are tightly connected, i. e., disks and clients are able to communicate with each other directly, with relatively uniform latency, and with relatively high reliability. This is in contrast to loosely connected peer-topeer and WAN networks in which communication latencies are longer and possibly highly varied. Our target environment is a corporate data center or scientific computing network, likely dedicated to storage traffic.

RUSH 变体之所以能够提供如此高的灵活性和性能，部分原因在于它们对 OSD 和客户端的结构做出了假设。首先，我们假设磁盘和客户端紧密连接，即磁盘和客户端能够直接通信，延迟相对均匀，可靠性也相对较高。这与松散连接的点对点网络和 WAN 网络形成了对比，在这些网络中，通信延迟更长，而且可能变化很大。我们的目标环境是企业数据中心或科学计算网络，可能专用于存储流量。

Another important assumption crucial to the functioning of RUSH is that disks are added to the system in homogeneous groups. A group of disks, called a sub-cluster have the same vintage and therefore share both performance and reliability characteristics. It is possible to add disks with different characteristics at the same time—they must merely be grouped into multiple homogeneous subclusters.

RUSH 运行的另一个重要假设是，磁盘以同构组的形式添加到系统中。一组磁盘（称为子集群）具有相同的年份，因此具有相同的性能和可靠性特性。可以同时添加具有不同特性的磁盘——只需将它们分组到多个同构子集群中即可。

All of the RUSH variants are described in pseudo-code later in this section; the symbols used in the pseudo-code and the accompanying explanations are listed in Table 1.

本节后面将以伪代码描述所有 RUSH 变体；伪代码中使用的符号及其附带的解释列于表 1 中。

Table 1. Symbols used in RUSH pseudo-code and explanations.

2.2、RUSH 概念

There are several common features of the RUSH variants which combine to allow scalability, flexibility and performance. The first of these is the recognition that as large storage systems expand, new capacity is typically added several disks at a time, rather than by adding individual disks. The use of sub-clusters leads naturally to a two-part lookup process: first, determine the sub-cluster in which an object belongs, and then determine which disk in the subcluster holds that object. This two part lookup allows us to mix and match different sub-cluster mapping algorithms and different disk mapping algorithms, in order to provide the best feature set for a particular problem.

RUSH 变体具有多种共同特性，这些特性结合在一起实现了可扩展性、灵活性和性能。首先，我们认识到，随着大型存储系统的扩展，新容量通常是一次性添加多个磁盘，而不是逐个添加磁盘。子集群的使用自然会引发一个由两部分组成的查找过程: 首先，确定对象所属的子集群，然后确定子集群中哪个磁盘保存该对象。这种由两部分组成的查找过程使我们能够混合搭配不同的子集群映射算法和不同的磁盘映射算法，从而为特定问题提供最佳的特征集。

All of the RUSH variants are structured recursively. This recursive structure arises from the recursive nature of adding disks to an existing system: a system naturally divides into the most recently added disks, and the disks that were already in the system when they were added. RUSHp and RUSHr follow this model closely, while RUSHt applies a divide and conquer approach. Although the pseudocode is recursive, real implementations may be iterative in order to avoid the function call overhead.

所有 RUSH 变体都是递归结构的。这种递归结构源于向现有系统添加磁盘: 系统会自然地划分为最近添加的磁盘和添加时系统中已有的磁盘。RUSHp 和 RUSHr 严格遵循此模型，而 RUSHt 则采用分而治之的方法。虽然伪代码是递归的，但实际实现可能会采用迭代方式，以避免函数调用开销。

Probabilistic placement of objects also seems like a natural choice for RUSH because many hash functions offer excellent performance and even distribution of objects, . Probabilistic placement also facilitates weighting of subclusters and the distribution of replicas of a particular object evenly throughout the system.

对于 RUSH 来说，对象的概率放置似乎也是一个自然的选择，因为许多哈希函数提供了出色的性能和均匀的对象分布。概率放置还有助于对子集群进行加权，并在整个系统中均匀分布特定对象的副本。

All of the RUSH variants use a parametric hash with two additional parameters. The hash function is a simple multiplicative hash which yields values in the range [0,1): h(k) = Ak mod 1 where A ∈ [0,1).

所有 RUSH 变体都使用带有两个附加参数的参数哈希函数。哈希函数是一个简单的乘法哈希，其值在 [0, 1] 范围内: h(k) = Ak mod 1，其中 A ∈ [0, 1)。

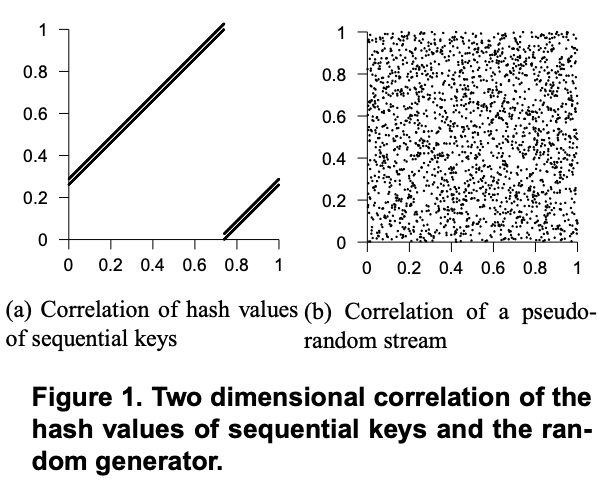
Unfortunately, a simple multiplicative hash function generates a highly correlated sequence of randomlydistributed hash values when its parameters are sequential, as shown in Figure 1(a). Since RUSH requires that hash values be well-distributed regardless of parameter sequentiality, we use a simple hash function on one parameter to seed a random number generator and then use the stream of resulting values as random numbers. The output of the generator is shown in Figure 1(b).

遗憾的是，当一个简单的乘法哈希函数的参数是连续的时，它会生成一个高度相关的随机分布的哈希值序列，如图 1(a) 所示。由于 RUSH 要求哈希值必须均匀分布，而与参数的连续性无关，因此我们使用一个参数上的简单哈希函数作为随机数生成器的种子，然后将生成的值流用作随机数。生成器的输出如图 1(b) 所示。

Figure 1. Two dimensional correlation of the hash values of sequential keys and the random generator.

2.3、RUSHp : 使用素数进行放置

RUSHp is described in detail in our previous work [10] so we will only briefly discuss this algorithm. The algorithm for RUSHp, using symbols described in Table 1 is shown in Figure 2.

我们在前文[10]中对 RUSHp 算法进行了详细描述，因此本文仅简要讨论该算法。RUSHp 算法使用表 1 中描述的符号，如图 2 所示。

Figure 2. Pseudo-code for RUSHp.

RUSHp takes a key and replica id and returns a disk id. It first decides in which sub-cluster an object replica belongs by computing the parametric hash of an object. It compares the hash value, which is in the range [0,1), to the ratio of the amount of weight in the most recently added sub-cluster to the total weight in the system. If the hash value is less than the ratio of weights, the object replica belongs in the most recently added sub-cluster. Otherwise, the object must belong in one of the previously added sub-clusters, so RUSHp discards the most recently added sub-cluster and repeats the process.

RUSHp 接收一个 key 和 replica id ，并返回一个 disk id。它首先通过计算对象的参数哈希来确定对象副本属于哪个子集群。它将哈希值（范围为 [0, 1)）与最新添加的子集群的权重占系统总权重的比例进行比较。如果哈希值小于权重比例，则对象副本属于最新添加的子集群。否则，该对象必须属于先前添加的子集群之一，因此 RUSH 会丢弃最新添加的子集群并重复该过程。

Once RUSHp decides on the sub-cluster in which an object replica belongs, it places the object replica in some disk in the sub-cluster using the function $f(x,r) = z + rp( mod m_j)^1$ , where $z$ is essentially a hash of the key $x$, $p$ is a randomly chosen prime number, and $m_j$ is the number of disks in the sub-cluster.

一旦 RUSHp 确定了对象副本所属的子集群，它就会使用函数 $f(x,r) = z + rp( mod m_j)^1$ 将对象副本放置在子集群中的某个磁盘中，其中 $z$ 本质上是密钥 $x$ 的哈希值， $p$ 是随机选择的素数， $m_j$ 是子集群中的磁盘数量。

With a few simple number theory lemmas we can show that as long as $r$ is less than or equal to $m_j$ , $f(x,r_i) \neq f(x,r_k)$ for $i \neq k$. Using a more advanced analytic number theory result called the Prime Number Theorem for Arithmetic Progressions [9], we can show that this function will distribute the replicas of object $x$ in $m_jφ(m_j)$ different $arrangements^2$ , and each arrangement is equally likely.

利用几个简单的数论引理，我们可以证明，只要 r 小于或等于 m，当 i = 6 = k 时，f (x, r) = f (x, r)。利用一个更高级的解析数论结果——算术级数的素数定理 [9]，我们可以证明，该函数会将对象 $x$ 的副本分布在 $m_jφ(m_j)$ 种不同的排列中，并且每种排列的可能性均等。

Note that, in most cases, a single sub-cluster will not contain all of the replicas of an object. However, there is a finite probability of this occurring, and it indeed will always happen if there is only one sub-cluster, so the algorithm must allow for this possibility. RUSHp uses a trick to allow all of the sub-clusters except for the original subcluster to have fewer disks than the object replication factor, as described in our original paper on RUSHp [10].

请注意，在大多数情况下，单个子集群不会包含对象的所有副本。然而，这种情况发生的概率是有限的，而且如果只有一个子集群，这种情况确实总是会发生，因此算法必须考虑到这种可能性。 RUSHp 使用了一种技巧，允许除原始子集群之外的所有子集群的磁盘数量都少于对象副本因子，正如我们在 RUSHp 的原始论文[10]中所述。

2.4、RUSHr : 支持移除

RUSHr differs from RUSHp in that it locates all of the replicas of an object simultaneously, allowing sub-clusters to be removed or reweighted without reorganizing the entire system. RUSHr uses the same ratio that RUSHp uses in order to determine which objects go where: the ratio between the number of servers in the most recently added sub-cluster and the number of servers in the whole system. These values, however are passed separately as parameters to a draw from the hypergeometric distribution3 . The result of the draw is the number of replicas of the object that belong in the most recently added sub-cluster, as shown in Figure 3(a).

RUSHr 与 RUSHp 的不同之处在于，它会同时定位一个对象的所有副本，从而允许在不重组整个系统的情况下移除或调整子集群的权重。 RUSHr 使用与 RUSHp 相同的比率来确定哪些对象应该被分配到哪里: 即最近添加的子集群中的服务器数量与整个系统中服务器数量的比率。然而，这些值会作为参数单独传递给超几何分布的抽取函数。抽取的结果是属于最近添加的子集群的对象的副本数量，如图 3(a) 所示。

Once the number of replicas that belong in the most recently added sub-cluster has been determined, we use a simple technique, shown in Figure 3(b), to randomly draw the appropriate number of disk identifiers.

一旦确定了属于最近添加的子集群的副本数量，我们将使用一种简单的技术（如图 3(b) 所示）随机抽取适当数量的磁盘标识符。

Figure 3. Pseudo-code for the RUSHr algorithm.

2.5、RUSHt: 基于树的方法

RUSHt was devised to increase the scalability of RUSH by allowing computation time to scale logarithmically with the number of sub-clusters in the system. It also offers more flexibility in the ways in which a system can be reorganized. It accomplishes this with some sacrifice in the competitiveness of its reorganizations, as described in Section 3.4.

RUSHt 的设计目的是通过允许计算时间随系统中子集群数量呈对数增长来提高 RUSH 的可扩展性。它还为系统重组的方式提供了更大的灵活性。如第 3.4 节所述，它以牺牲重组的竞争力为代价来实现这一点。

RUSHt is similar to RUSHp, except that it uses a binary tree data structure rather than a list. Each node in the tree knows the total weight to the left and right of the node, and each nodes has a unique identifier which is used as a parameter to the hash function.

RUSHt 与 RUSHp 类似，不同之处在于它使用二叉树数据结构而非列表。树中的每个节点都知道其左右两侧的总权重，并且每个节点都有一个唯一的标识符，用作哈希函数的参数。

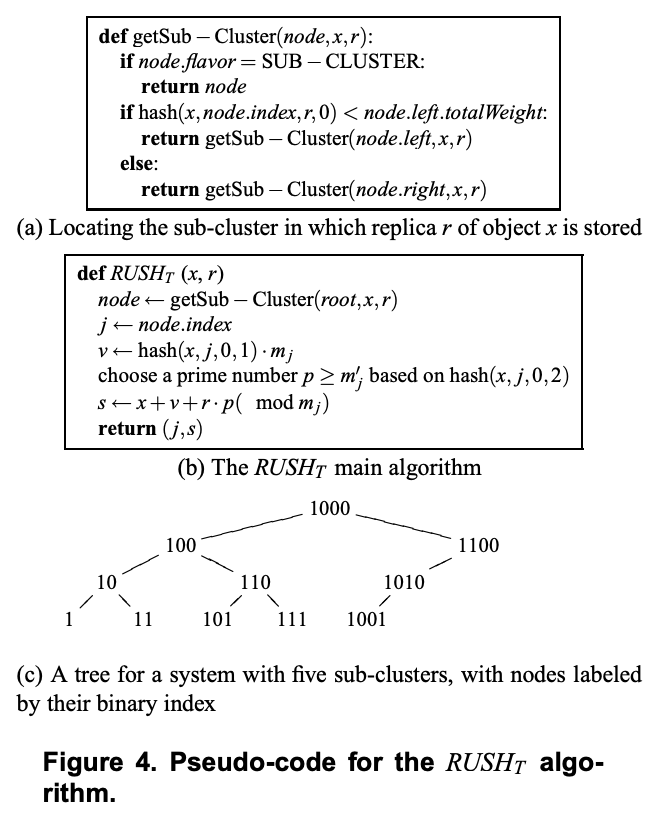
As with the other RUSH variants, RUSHt first looks up the sub-cluster in which an object replica belongs. The RUSHt algorithm, shown in Figure 4(b) accomplishes this by calculating the hash of the key of the object, parameterized by the unique index of the current node (starting with the root). RUSHt then compares this hash value to the ratio between the amount of weight to the left of the current node and the total amount of weight to the left and right of the node. If the hash value is less than this ratio, then the object belongs to the left of the current node, otherwise, it belongs to the right. This process is repeated until a sub-cluster leaf node is reached.

与其他 RUSH 变体一样，RUSHt 首先查找对象副本所属的子集群。图 4(b) 所示的 RUSHt 算法通过计算对象键的哈希值来实现此目的，该哈希值由当前节点的唯一索引（以根节点）。然后，RUSHt 将此哈希值与当前节点左侧的权重与该节点左右两侧权重总和的比率进行比较。如果哈希值小于该比率，则该对象属于当前节点的左侧，否则属于右侧。此过程重复进行，直至到达子集群的叶节点。

Figure 4. Pseudo-code for the RUSHT algorithm.

A tree illustrating the result of this process for a system with five subclusters is show in Figure 4(c).

图 4(c) 显示了具有五个子集群的系统的此过程的结果。

Once the replica’s sub-cluster has been found, RUSHt then determines the specific server in the sub-cluster on which to place the object replica in the same way that RUSHp does, described in Section 2.3. The technique used in RUSHp for allowing sub-clusters to be smaller than the replication factor does not work, however, for RUSHt ; this is perhaps the main drawback of RUSHt.

一旦找到副本的子集群，RUSHt 就会按照 2.3 节中描述的方式，确定子集群中放置对象副本的具体服务器。然而，RUSHp 中允许子集群小于复制因子的技术在 RUSHt 中并不适用；这或许是 RUSHt 的主要缺点。

When a system gains additional sub-clusters or is otherwise reorganized, RUSHt must ensure that nodes in the tree always have the same unique identifier. This is done by allocating binary identifiers starting with the leftmost leaf (the original sub-cluster in the system), allocating that leaf the identifier “1”. To add a new root node, shift the root’s identifier one bit to the left, copy the identifiers from the left subtree to the right subtree, and append a “1” on the left hand side of every identifier in the right hand subtree, pruning off any unused branches.4 A tree illustrating the result of this process for a system with five sub-clusters is show in Figure 4(c).

当系统获得额外的子集群或进行重组时， RUSHt 必须确保树中的节点始终具有相同的唯一标识符。这是通过从最左边的叶子节点（系统中的原始子集群）开始分配二进制标识符来实现的，并为该叶子节点分配标识符 “1”。要添加新的根节点，请将根节点的标识符向左移动一位，将左子树中的标识符复制到右子树，并在右子树中每个标识符的左侧添加一个 “1”，并修剪掉所有未使用的分支。下图展示了图 4(c) 显示了具有五个子集群的系统的该过程的结果。

3、RUSH 实践

Since the RUSH family of algorithms was designed to allocate data in petabyte-scale storage systems, we measured its behavior under different situations to show that RUSH does, indeed, meet its design goals. In this section we describe a series of experiments that illustrate various characteristics of each of the RUSH variants. All measurements were performed on a 2.8 GHz Pentium 4 machine.

由于 RUSH 系列算法旨在在 PB 级存储系统中分配数据，我们测量了其在不同情况下的行为，以证明 RUSH 确实达到了其设计目标。本节将描述一系列实验，以说明 RUSH 各个变体的不同特性。所有测量均在 2.8 GHz Pentium 4 计算机上进行。

3.1、对象查找性能

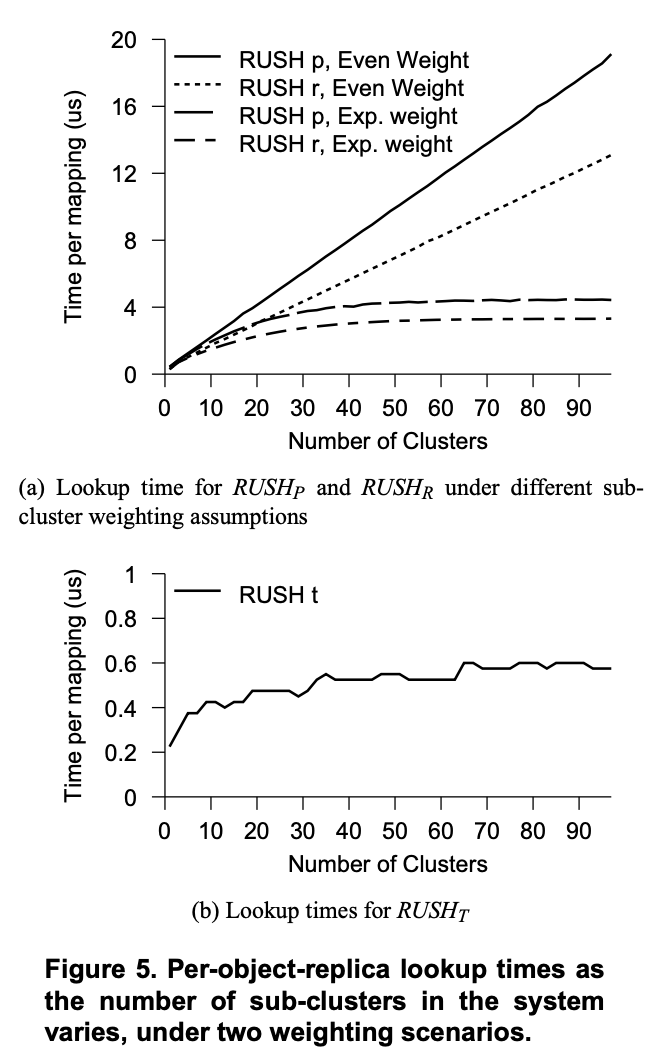
In our first experiment, we examine the performance characteristics of RUSH. Informally, in the worst case, RUSHp and RUSHr must iterate over every sub-cluster in the system, doing a constant amount of work in each subcluster, so the lookup time of RUSHp and RUSHr grows linearly with the number of sub-clusters in the system. RUSHt on the other hand, uses a binary tree to locate the correct sub-cluster, again doing constant work at each node, so lookup time is logarithmic in the number of sub-clusters in the system.

在我们的第一个实验中，我们考察了 RUSH 的性能特征。通俗地说，在最坏的情况下，RUSHp 和 RUSHr 必须遍历系统中的每个子集群，在每个子集群中执行恒定的工作量，因此 RUSHp 和 RUSHr 的查找时间会随着系统中子集群的数量线性增长。另一方面，RUSHt 使用二叉树来定位正确的子集群，同样在每个节点上执行恒定的工作量，因此查找时间与系统中子集群的数量呈对数关系。

The lookup time for RUSHp and RUSHr, however, also varies depending on the weighting in the system. If the most recently added disks have higher weight than previously added disks, then the lookup process will tend to stop after only examining the most recently added sub-clusters. Since newer disks will tend to have greater capacity and and throughput, we expect newer disks to have higher weight, and thus we expect the performance of RUSHp and RUSHr to be sub-linear.

然而，RUSHp 和 RUSHr 的查找时间也会根据系统中的权重而变化。如果最近添加的磁盘比之前添加的磁盘具有更高的权重，那么查找过程往往会在仅检查最近添加的子集群后停止。由于较新的磁盘往往具有更大的容量和吞吐量，我们预计较新的磁盘将具有更高的权重，因此我们预计 RUSHp 和 RUSHr 的性能将是亚线性的。

Since RUSHt must always traverse a tree regardless of the weightings of the sub-clusters in the system, weighting does not affect the performance of RUSHt . This may be advantageous in systems where quality of service guarantees are important.

由于 RUSHt 必须始终遍历树，而不管系统中子集群的权重如何，因此权重不会影响 RUSHt 的性能。这在注重服务质量保证的系统中可能具有优势。

To perform the experiments in this section, we started with a system with only a single sub-cluster. We then looked up four million object replicas, and took the average time for a lookup. Two more sub-clusters were added, and the process repeated; this was done until we reached 100 sub-clusters. Figure 5(a) shows the performance of RUSHp and RUSHr where each sub-cluster has the same weight, and where the weight in each sub-cluster increases exponentially, by a factor of 1.1. Figure 5(b) shows the shape of the performance curve for RUSHt . As expected, lookup times for RUSHt increased logarithmically with the number of sub-clusters in the system. The timing is so much faster than RUSHp and RUSHr that it does not show up on Figure 5—lookups required less than one microsecond even after 100 clusters had been added. The unevenness of the RUSHt line is due to the limited resolution of the timer on our system. If performance is an issue, mappings done by RUSHp and RUSHr can be cached because mappings of object replicas to disks do not change unless the system configuration is changed.

为了执行本节中的实验，我们首先从只有一个子集群的系统开始。然后，我们查找了四百万个对象副本，并计算了平均查找时间。之后，我们又添加了两个子集群，并重复此过程；直到达到 100 个子集群。图 5(a) 展示了 RUSHp 和 RUSHr 的性能，其中每个子集群具有相同的权重，并且每个子集群中的权重呈指数增长，增加 1.1 倍。图 5(b) 展示了 RUSHt 性能曲线的形状。正如预期的那样，RUSHt 的查找时间随着系统中子集群数量的增加而呈对数增长。其时间比 RUSHp 和 RUSHr 快得多，以至于在图 5 中没有体现出来——即使在添加了 100 个集群之后，查找时间也仅需不到一微秒。RUSHt 曲线的不均匀是由于我们系统上计时器的分辨率有限造成的。如果性能是一个问题，RUSHp 和 RUSHr 完成的映射可以被缓存，因为映射除非系统配置发生变化，否则对象副本到磁盘的数量不会改变。

Figure 5. Per-object-replica lookup times as the number of sub-clusters in the system varies, under two weighting scenarios.

3.2、对象分布

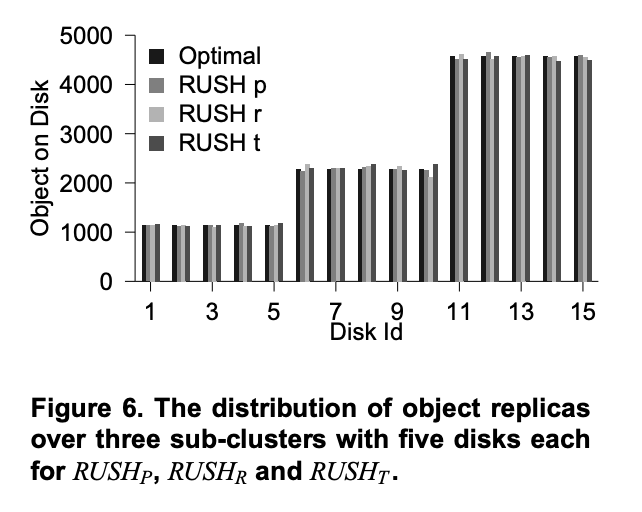
In this experiment, we tested the ability of RUSH to distribute objects according to a distribution of weights over sub-clusters. We inserted 10,000 objects with 4 replicas each into 3 sub-clusters of 5 disks each. Each sub-cluster has twice the weight of the sub-cluster to its left.

在本实验中，我们测试了 RUSH 根据子集群权重分布来分配对象的能力。我们将 10,000 个对象（每个对象包含 4 个副本）插入到 3 个子集群（每个集群包含 5 个磁盘）。每个子集群的权重是其左侧子集群的两倍。

Figure 6 shows the results of this experiment. Even with only 40,000 object replicas, all of the RUSH variants place objects almost exactly according to the appropriate weight. The leftmost bar in the figure shows the ideal value; none of the RUSH variants differ greatly from this ideal distribution.

图 6 展示了本次实验的结果。即使只有 40,000 个对象副本，所有 RUSH 变体也几乎完全按照适当的权重放置对象。图中最左侧的柱状图显示了理想值；所有 RUSH 变体与该理想分布均无太大差异。

Figure 6. The distribution of object replicas over three sub-clusters with five disks each for RUSHp, RUSHr and RUSHt.

3.3、故障恢复能力

In this experiment, we studied the behavior of the system when a disk fails. When a disk fails, the disks which hold replicas of the objects stored on the failed disk must service requests which would have been serviced by the failed disk. In addition, these disks must devote some percentage of their resources to failure recovery once the failed disk has been replaced. We call this extra workload failure load.

在本实验中，我们研究了磁盘发生故障时系统的行为。当磁盘发生故障时，保存故障磁盘上对象副本的磁盘必须处理原本由故障磁盘处理的请求。此外，在故障磁盘被替换后，这些磁盘必须投入一定比例的资源用于故障恢复。我们称之为额外的工作负载故障负载。

The more evenly distributed the replicas of objects from the failed disk, the more evenly distributed the failure load. In order to minimize service degradation and cascading failures, RUSH distributes the replicas of objects on a particular disk over the entire system. These replicas are distributed according the weights of each sub-cluster. We call the distribution of replicas of objects stored on the failed disk the failure distribution.

故障磁盘上对象的副本分布越均匀，故障负载分布就越均匀。为了最大限度地降低服务降级和级联故障，RUSH 将特定磁盘上对象的副本分布到整个系统。这些副本根据每个子集群的权重进行分布。我们将故障磁盘上存储的对象副本分布称为故障分布。

Figure 7 shows the failure distribution for disk 8 in a system with 3 sub-clusters of 5 disks each, all evenly weighted. Both RUSHp and RUSHt show a slight tendency to favor disks that are close to the failed disk, while RUSHr shows no such tendency. For comparison, we also examined a system in which the all the replicas of an object are allocated to four adjacent disks. For example, replicas of some object might be distributed to disks 8, 9, 10, and 11. In such a system, when disk 8 fails, replicas of the objects on disk 8 could be located on disks 5, 6, 7, 9, 10 or 11. In comparison to the system that places replicas on adjacent disks, the “favoritism” showed by RUSHp and RUSHt is almost negligible. In systems with more disks and more objects, the favoritism is even less pronounced, especially when compared to a system that distributes replicas to adjacent disks regardless of how many servers are in the system.

图 7 显示了具有 3 个子集群（每个集群有 5 个磁盘，所有磁盘的权重均等）的系统中磁盘 8 的故障分布。RUSHp 和 RUSHt 都略微倾向于选择靠近故障磁盘的磁盘，而 RUSHr 则没有这种倾向。为了进行比较，我们还研究了一个系统，其中某个对象的所有副本都分配给四个相邻的磁盘。例如，某个对象的副本可能分布到磁盘 8、9、10 和 11。在这样的系统中，当磁盘 8 发生故障时，磁盘 8 上对象的副本可能位于磁盘 5、6、7、9、10 或 11 上。与将副本放置在相邻磁盘上的系统相比，RUSHp 和 RUSHt 表现出的 “偏袒” 几乎可以忽略不计。在具有更多磁盘和更多对象的系统中，这种偏袒就不那么明显了，尤其是与无论系统中有多少台服务器都将副本分发到相邻磁盘的系统相比时。

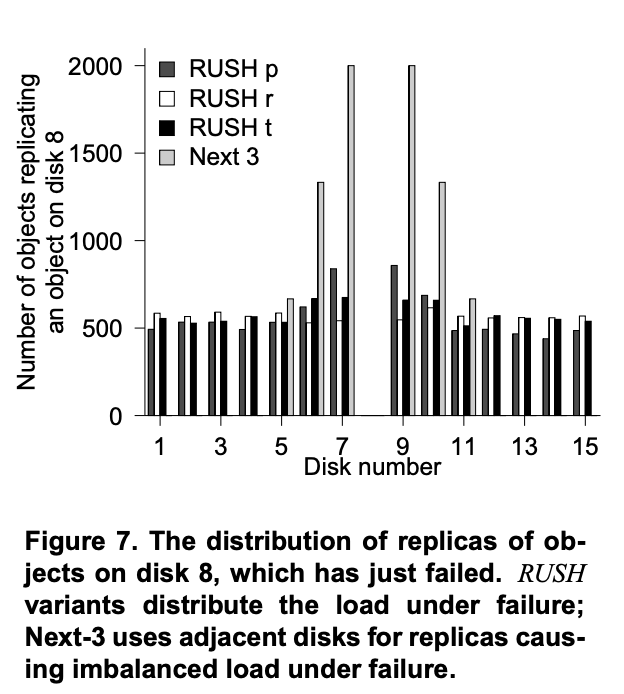
Figure 7. The distribution of replicas of objects on disk 8, which has just failed. RUSH variants distribute the load under failure; Next-3 uses adjacent disks for replicas causing imbalanced load under failure.

Unfortunately, the deviation from the optimal value depends on several complex factors and is therefore difficult to quantify. In RUSHp and RUSHt , the amount of the devi ation depends partly on the number unique coprimes of the size the sub-cluster in which the failure occurred, known as the Euler Totient Function. Despite this difficulty in quantifying the variance, we can see empirically that RUSHr gives the most faithful failure distribution, but that RUSHp and RUSHt are both extremely accurate. Figure 7 is representative of our findings for other system configurations.

不幸的是，与最优值的偏差取决于几个复杂的因素，因此很难量化。在 RUSHp 和 RUSHt 中，偏差量故障分布的准确性部分取决于发生故障的子集群大小的唯一互质数，即欧拉函数。尽管量化方差存在困难，但我们可以通过经验看出，RUSHr 给出了最可靠的故障分布，但 RUSHp 和 RUSHt 都极其准确。图 7 代表了我们对其他系统配置的发现。

3.4、重组

The final experiments described in this paper examined the number of objects that move during four different reorganization scenarios. In the first scenario, a sub-cluster is added to the system. In the second, a single disk is removed from the system, causing the number of disks in a sub-cluster to be adjusted. In the third scenario, the weight of a sub-cluster is increased. In the fourth scenario, an entire sub-cluster is removed from the system. In each of the experiments, the system starts with six sub-clusters with 4 disks each. We added 10,000 objects, each having 4 replicas, and then reorganized the system, counting the number of objects which moved during the reorganization.

本文描述的最终实验考察了四种不同重组场景下移动的对象数量。在第一种场景中，系统添加了一个子集群。在第二种场景中，从系统中移除一个磁盘，导致子集群中的磁盘数量发生调整。在第三种场景中，增加了一个子集群的权重。在第四种场景中，从系统中移除了一个完整的子集群。在每个实验中，系统初始包含六个子集群，每个集群包含 4 个磁盘。我们添加了 10,000 个对象，每个对象包含 4 个副本，然后重组系统，并计算重组期间移动的对象数量。

As shown in Figure 8, RUSHp and RUSHr both perform optimally when a sub-cluster is added to the system; in fact, they are theoretically optimal, so any variation is due to small variations in probabilistic distribution. RUSHt is slightly sub-optimal, but is consistently within a small constant factor of the optimal case.

如图 8 所示，当系统中添加子集群时，RUSHp 和 RUSHr 的性能均达到最佳；事实上，它们在理论上是最优的，因此任何变化都是由概率分布的微小变化引起的。RUSHt 略微次优，但始终在最优情况的一个小常数因子范围内。

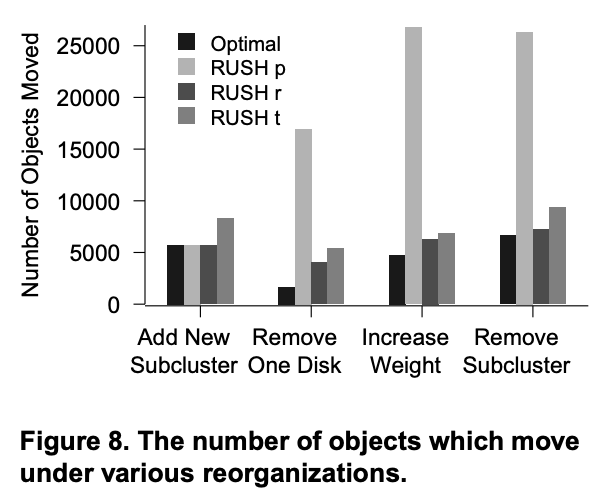
Figure 8. The number of objects which move under various reorganizations.

RUSH was not designed for a system in which individual disks are removed, as is apparent from the second column in Figure 8. While RUSHr and RUSHt move about three times as many objects as the optimal number, RUSHp moves around ten times as many—over a third of the objects in the system! If removing a disk is necessary, and the number of objects moved is unacceptable, we can take advantage of RUSH’s adjustable replication factors by maintain a list of removed disks. If an object maps to any removed disk, increase its replication factor by one and look up the new replica instead. This process may be repeated until an existing disk is found. While this mechanism clearly causes an optimal number of objects to be moved, it has some limitations. For example, RUSHp and RUSHt both have a maximum replication factor. Also, worst case lookup time increases linearly with the number of removed disks. A more in depth examination of this mechanism is the subject of future research.

RUSH 的设计初衷并非针对单个磁盘被移除的系统，这一点从图 8 的第二列就可以看出来。虽然 RUSHr 和 RUSHt 移动的物体数量是最佳数量的三倍，但 RUSHp 移动的对象数量大约是原来的十倍——超过系统中三分之一！如果需要移除磁盘，而移动的对象数量不可接受，我们可以利用 RUSH 的可调复制因子，维护一个已移除磁盘的列表。如果某个对象映射到任何已移除的磁盘，则将其复制因子增加一，并查找新的副本。此过程可能会重复，直到找到现有磁盘。虽然这种机制显然会导致移动的对象数量达到最佳，但它也有一些局限性。例如，RUSHp 和 RUSHt 都有一个最大复制因子。此外，最坏情况下的查找时间会随着已移除磁盘的数量线性增加。对这种机制的更深入研究是未来研究的主题。

The third column of Figure 8 shows that RUSHt and RUSHr perform well when the weight of an entire subcluster is increased, but RUSHp again performs poorly. In both adding (column 3) and removing weight (column 4) from a sub-cluster, RUSHt and RUSHr both perform well, whereas RUSHp does not. This behavior is expected, since RUSHt and RUSHr were designed to allow changing subcluster weights, whereas RUSHp was not.

图 8 的第三列显示，当整个子簇的权重增加时，RUSHt 和 RUSHr 表现良好，但 RUSHp 再次表现不佳。在添加（第 3 列）和从子簇中移除权重（第 4 列）时，RUSHt 和 RUSHr 均表现良好，而 RUSHp 则表现不佳。这种行为是可以预料的，因为 RUSHt 和 RUSHr 的设计允许更改子簇权重，而 RUSHp 则不允许。

4、RUSH 的应用

Each RUSH variant excels in a different environment. While RUSHt offers the best performance and the best overall flexibility in reconfiguration, it does not allow subclusters smaller than the maximum number of a replicas that a single object may have. It also moves more than the optimal number of objects during reorganization, though the number is within a small factor of the optimal number of objects. RUSHt is thus best suited for very large systems in which disks will be added in large numbers. However, for systems which the designers intend to build by adding a very small number of disks at a time (small scale systems) or systems that will be reorganized continuously, one of the other RUSH variants may be better.

每种 RUSH 变体在不同的环境中都有其优势。虽然 RUSHt 在重新配置方面提供了最佳性能和最佳整体灵活性，但它不允许子集群小于单个对象的最大副本数。在重组过程中，它移动的对象数量也会超过最佳数量，尽管该数量与最佳对象数量相差无几。因此，RUSHt 最适合需要大量添加磁盘的大型系统。然而，对于设计人员打算通过一次添加少量磁盘来构建的系统（小型系统），RUSHt 并不适用。或者将不断重组的系统，其他 RUSH 变体之一可能会更好。

RUSHr also provides significant flexibility, but at the cost of performance. Since RUSHr performance degrades linearly with the number of sub-clusters in the system, it is not well suited to a system where sub-clusters are added or removed frequently. It also cannot support systems where each “replica” in a replica group is actually a distinct entity rather than an exact copy, as would be the case if “replicas” were used as part of an erasure coding scheme. On the other hand, because RUSHr does not rely on the number theory behind RUSHp and RUSHt , it can allow any replication factor up to the total number of disks in the system. This means that a system using RUSHr has more flexibility in the number of disks that can be removed from the system individually using the mechanism discussed in Section 3.4. It also has more flexibility to use a “fast mirroring copy” technique [21] to increase the mean time to data loss in a system.

RUSHr 也提供了显著的灵活性，但却以牺牲性能为代价。由于 RUSHr 的性能会随着系统中子集群数量的增加而线性下降，因此它不太适合频繁添加或删除子集群的系统。它也无法支持副本组中的每个 “副本” 实际上是一个独立实体而非精确副本的系统（如果 “副本” 被用作纠删码方案的一部分，情况就会如此）。另一方面，由于 RUSHr 不依赖于 RUSHp 和 RUSHt 背后的数论，它可以允许任意复制因子，最高可达系统中磁盘的总数。这意味着使用 RUSHr 的系统在使用 3.4 节中讨论的机制从系统中单独移除的磁盘数量方面具有更大的灵活性。它还可以更灵活地使用 “快速镜像复制” 技术 [21] 来增加系统中数据丢失的平均时间。

RUSHp offers similar behavior to RUSHr, except that it supports erasure coding. This ability comes at the expense of not being able to remove sub-clusters once they are added (without significant reorganization costs). RUSHp also requires that the replication factor in the system be less than or equal to the number of disks in the first sub-cluster added to the system, but subsequent sub-clusters need not have sufficient disks to hold all of the replicas of a single object on unique disks. In that respect, it is more flexible than RUSHt , but less flexible than RUSHr.

RUSHp 的行为与 RUSHr 类似，但前者支持纠删码。此功能的代价是，一旦添加子集群，就无法移除（无需大量的重组成本）。RUSHp 还要求系统中的复制因子小于或等于添加到系统的第一个子集群的磁盘数量，但后续子集群无需拥有足够的磁盘空间来将单个对象的所有副本存储在唯一的磁盘上。从这个方面来看，它比 RUSHt 更灵活，但不如 RUSHr 灵活。

Because RUSHt’s performance does not depend on the weighting of the sub-clusters, and objects on every subcluster can be located in the same amount of time, RUSHt can make better quality of service guarantees.

由于 RUSHt 的性能不依赖于子集群的权重，并且每个子集群上的对象都可以在相同的时间内被定位，因此 RUSHt 可以做出更好的服务质量保证。

Table 2 gives a side-by-side comparison of the features of the RUSH variants and Linear Hashing variants [14], simple hashing, and a tabular, or “directory” approach. An “X” indicates that the algorithm supports the feature and “- “ indicates that it supports the feature under some circumstances. The “tabular” approach keeps a centralized table, possibly cached in part on the clients, containing pointersto all of the object replicas. It has “-“ instead of “X” because the approach neither rules out nor ensures any of these features. In fact, RUSH could be used to generate and maintain the table in such a system. Any such system has the same constraints to RUSH: it must guarantee that no two replicas of the same object are on the same disk and support weighting.

表 2 并排比较了 RUSH 变体与线性哈希变体 [14]、简单哈希以及表格或 “目录” 方法的特性。”X” 表示该算法支持该特性， “” 表示在某些情况下支持该特性。 “表格” 方法维护一个集中式表，可能部分缓存在客户端上，其中包含指向所有对象副本的指针。它用 “-“ 而不是 “X” 是因为该方法既不排除也不保证任何这些特性。事实上， RUSH 可用于在这样的系统中生成和维护表格。任何这样的系统都有与 RUSH 相同的约束: 它必须保证同一对象的任何两个副本不会位于同一磁盘上，并且支持加权。

Table 2. Features of RUSH and three other related algorithms/distribution mechanisms. SH refers to simple hashing, and Tab is a simple tabular approach.

We conclude this section by giving a brief example of a system best suited to each of the RUSH variants. In a small system such as a small storage server or a replicated object database, the user does not necessarily want to add several disks or servers at once. In that case RUSHp or RUSHr is more appropriate. In the case of a small storage server, storage space is typically a more important issue that in an object database, where transaction speed is often more important. For that reason, RUSHp, which supports erasure coding, is probably more suited to a small storage server, whereas RUSHr is probably more suited to an object database because of the added flexibility in configuration. Large storage systems, on the other hand, typically add many disks at once, and therefore are not constrained by the need to add a minimum numbers of disks to the system at once. Very large storage clusters are also typically very performance sensitive. Because RUSHt provides the best performance both in terms of lookup times and reorganizations, and because of its flexibility in configuration and reconfiguration, RUSHt is most appropriate for very large storage systems, such as the one we are designing in the Storage Systems Research Center at the University of California, Santa Cruz.

我们将通过简要介绍最适合每种 RUSH 变体的系统示例来结束本节。在小型系统（例如小型存储服务器或复制对象数据库）中，用户不一定希望一次添加多个磁盘或服务器。在这种情况下，RUSHp 或 RUSHr 更为合适。对于小型存储服务器，存储空间通常比对象数据库更重要，因为对象数据库的事务速度通常更为重要。因此，支持纠删码的 RUSHp 可能更适合小型存储服务器，而 RUSHr 可能更适合对象数据库，因为它增加了配置灵活性。另一方面，大型存储系统通常会一次添加许多磁盘，因此不受一次向系统添加最少磁盘数量的限制。超大型存储集群通常也对性能非常敏感。由于 RUSHt 在查找时间和重组方面均提供了最佳性能，并且由于其在配置和重新配置方面的灵活性，因此 RUSHt 最适合非常大的存储系统，例如我们正在加州大学圣克鲁斯分校的存储系统研究中心设计的系统。

5、相关工作

The topic of Scalable Distributed Data Structures (SDDS) has received considerable attention. Litwin, et al. have developed many distributed variants of Linear Hashing which incorporate features such as erasure coding and security. The original LH* paper provides an excellent introduction to the LH* variants[14]. LH* unfortunately does not use disk space optimally [2], and results in a “hotspot” of disk and network activity during reorganizations. More importantly, LH* does not support weighting, and distributes data in such a way that increases the likelihood of correlated failures or performance degradations. Other data structures such as DDH [7] suffer from similar issues in utilizing space efficiently. Kr¨oll and Widmayer [12] propose tree-based SDDSs called Distributed Random Trees which allow for complex queries such as range queries. DRTs do not support data replication (although the authors discuss metadata replication), and their worst case performance is linear in the number of disks in the system. Litwinet al. also propose a B-Tree based family called RP* [13], which suffers from problems similar to LH*.

可扩展分布式数据结构 (SDDS) 的主题已获得广泛关注。Litwin 等人开发了许多分布式线性哈希变体，这些变体融合了纠删码和安全性等特性。最初的 LH* 论文对 LH* 变体进行了精彩的介绍[14]。遗憾的是，LH* 未能以最优方式利用磁盘空间 [2]，导致重组期间磁盘和网络活动出现 “热点” 。更重要的是，LH* 不支持加权，其数据分布方式增加了相关故障或性能下降的可能性。其他数据结构，例如 DDH [7]，在高效利用空间方面也存在类似的问题。Kr¨oll 和 Widmayer [12] 提出基于树的分布式随机树（SDDS）被称为分布式随机树（DRT），它允许执行诸如范围查询之类的复杂查询。DRT 不支持数据复制（尽管作者讨论了元数据复制），并且其最坏情况下的性能与系统中的磁盘数量呈线性关系。Litwin 等人还提出了一个基于 B 树的 RP* 家族[13]，它存在与 LH* 类似的问题。

Choy, et al. [5] describe algorithms for distributing data over disks which move an optimal number of objects as disks are added. These algorithms do not support weighting, replication, or disk removal. Brinkmann, et al. [3] propose a method to distribute data by partitioning the unit range. Their algorithm features 2-competitive reorganizations and supports weighting but not replication; it was extended by Wu and Burns [20] to map file sets, rather than files, to the unit range using a method similar to our technique of mapping objects to replica groups. SCADDAR [8] explored algorithms for assigning media blocks to disks in a system in which disks are added and removed. SCADDAR uses remapping functions similar in flavor to those in RUSH, but does not support replication beyond simple offset-based replication as discussed in Section 3.3. Consistent hashing [11] has many of the qualities of RUSH, but has a high migration overhead and is less well-suited to read-write file systems; Tang and Yang [18] use consistent hashing as part of a scheme to distribute data in large-scale storage clusters.

Choy 等人 [5] 描述了在磁盘上分发数据的算法，这些算法在添加磁盘时移动最佳数量的对象。这些算法不支持加权、复制或磁盘移除。Brinkmann 等人 [3] 提出了一种通过划分单位范围来分发数据的方法。他们的算法具有 2 竞争重组，支持加权但不支持复制；Wu 和 Burns [20] 对其进行了扩展，使用类似于我们将对象映射到副本组的技术的方法将文件集（而不是文件）映射到单位范围。SCADDAR [8] 探索了在添加和移除磁盘的系统中将介质块分配给磁盘的算法。SCADDAR 使用与 RUSH 类似的重映射函数，但不支持除 3.3 节中讨论的简单的基于偏移量的复制之外的复制。一致性哈希 [11] 具有 RUSH 的许多特性，但迁移开销很高，不太适合读写文件系统； Tang 和 Yang [18] 使用一致性哈希作为在大型存储集群中分发数据的方案的一部分。

Chau and Fu discuss algorithms to support graceful degradation of performance during failures in declustered RAID systems [4]. As discussed in Section 3.3, our algorithms also feature graceful degradation of performance during failures.

Chau 和 Fu 讨论了支持分簇 RAID 系统在故障期间性能优雅降级的算法 [4]。如 3.3 节所述，我们的算法也支持在故障期间性能优雅降级。

Peer-to-peer systems such as CFS [6], PAST [17], and Gnutella [16] assume that storage nodes are extremely unreliable. Consequently, data has a very high degree of replication. Furthermore, most of these systems make no attempt to guarantee long term persistence of stored objects. In some cases, objects may be “garbage collected” at any time by users who no longer want to store particular objects on their node, and in others, objects which are seldom used are automatically discarded. Because of the unreliability of individual nodes, these systems use replication for high availability, and are less concerned with maintaining balanced performance across the entire system. Other large scale persistent storage systems such as Farsite [1] and OceanStore [15] provide more file system-like semantics. Objects placed in the file system are guaranteed, within some probability of failure, to remain in the file system until they are explicitly removed. The inefficiencies introduced by the peer-to-peer and wide area storage systems address security, reliability in the face of highly unstable nodes, and client mobility, among other things. However, these features require too much overhead for a tightly coupled high-performance object storage system.

诸如 CFS [6]、PAST [17] 和 Gnutella [16] 之类的对等系统假设存储节点极不可靠。因此，数据具有极高的复制度。此外，大多数此类系统并未尝试保证存储对象的长期持久性。在某些情况下，对象可能会被不再希望在其节点上存储特定对象的用户随时”垃圾回收”；而在其他情况下，很少使用的对象会被自动丢弃。由于单个节点的不可靠性，这些系统使用复制来实现高可用性，而较少关注维护整个系统的均衡性能。其他大型持久性存储系统，例如 Farsite [1] 和 OceanStore [15]，则提供了更类似于文件系统的语义。在一定的故障概率内，放置在文件系统中的对象可以保证在被明确删除之前一直保留在文件系统中。点对点和广域存储系统带来的低效率问题，主要体现在安全性、在高度不稳定的节点下的可靠性以及客户端的移动性等方面。然而，对于紧密耦合的高性能对象存储系统来说，这些功能需要太多的开销。

6、未来工作

One problem with RUSH is that we do not yet know how to calculate the inverse—we can not directly answer the question, “which objects are stored on a given a disk?” We must instead iterate through all possible object identifiers and replica numbers and calculate the disk on which it belongs. We then simply discard all objects that do belong on the disk in question. Some preliminary research, however, suggests that it may be possible to invert RUSH, and enumerate the objects assigned to a particular server. This process involves solving a system of n linear equations, where n represents the number of comparisons necessary to locate the correct subcluster for an object.

RUSH 的一个问题是，我们尚不清楚如何计算它的逆——我们无法直接回答 “哪些对象存储在给定的磁盘上？” 这个问题。我们必须遍历所有可能的对象标识符和副本编号，并计算出它所属的磁盘。然后，我们直接丢弃所有确实属于该磁盘的对象。然而，一些初步研究表明，或许可以反转 RUSH ，并枚举分配给特定服务器的对象。这个过程涉及求解一个由 n 个线性方程组成的系统，其中 n 表示为某个对象找到正确子集群所需的比较次数。

We also would like to place theoretical bounds on the the number of objects which can move during a reorganization, and quantify the standard error in the number of objects stored on a particular disk.

我们还想对重组期间可以移动的对象数量设置理论界限，并量化特定磁盘上存储的对象数量的标准误差。

We are currently exploring different mechanisms for reducing the impact of removing a single disk either temporarily or permanently from the system.

我们目前正在探索不同的机制来减少从系统中暂时或永久移除单个磁盘的影响。

Finally, we are examining the utility of these algorithms for a broader class of applications including an object database and a searchable distributed web cache.

最后，我们正在研究这些算法对于更广泛的应用程序（包括对象数据库和可搜索的分布式网络缓存）的实用性。

7、结论

This paper has provided an overview of a family of algorithms we have developed to distribute objects over disks in a heterogeneous object based storage device. We describe three algorithms: RUSHp, RUSHr and RUSHt . These three algorithms all support weighting of disks, object replication, and near-optimal reorganization in may common scenarios.

本文概述了我们开发的一系列算法，用于在异构对象存储设备中将对象分布到磁盘上。我们描述了三种算法: RUSHp、RUSHr 和 RUSHt。这三种算法都支持磁盘加权、对象复制以及常见场景下的近乎最优的重组。

Our experiments show that while all three algorithms can perform lookups very quickly, RUSHt performs an order of magnitude faster in systems which have been reorganized several times. RUSHt also provides the best reorganization behavior under many conditions. This increased flexibility comes at some expense to the range of configurations which are possible for RUSHt . In particular, every subcluster in a system managed by RUSHt must have at least as many disks as an object has replicas. Since small systems will typically have small replication factors, this may or may not be an impediment. Clearly, however, RUSHt is the best algorithms for distributing data over very large clusters of disks.

我们的实验表明，虽然这三种算法都能非常快速地执行查找，但在经过多次重组的系统中，RUSHt 的执行速度要快一个数量级。RUSHt 在许多条件下也提供了最佳的重组行为。这种灵活性的提升是以牺牲 RUSHt 的配置范围为代价的。具体来说，RUSHt 管理的系统中的每个子集群必须至少拥有与对象副本数量相同的磁盘数量。由于小型系统通常副本数较小，这可能会或可能不会成为障碍。然而，显然，RUSHt 是将数据分布到超大型磁盘集群的最佳算法。

RUSHp and RUSHr both provide alternatives to RUSHt for smaller systems. Since it has the greatest flexibility in configurations RUSHr may be the best option for systems which need to remove disks one at a time from the system. Because it supports erasure coding, RUSHp may be the best option for smaller systems where storage space is at a premium.

RUSHp 和 RUSHt 都为小型系统提供了 RUSHt 的替代方案。由于 RUSHr 具有最大的灵活性，对于需要逐个移除磁盘的系统，RUSHr 可能是最佳选择。由于支持擦除编码，RUSHp 可能是存储空间有限的小型系统的最佳选择。

RUSH algorithms operate well across a wide range of scalable storage systems. By providing support for replication, system growth and disk obsolescence, and totally decentralized lookup, RUSH enables the construction of highperformance, highly parallel object-based storage systems.

RUSH 算法在各种可扩展存储系统上运行良好。通过提供对复制、系统增长和磁盘淘汰的支持以及完全去中心化的查找，RUSH 能够构建高性能、高度并行的基于对象的存储系统。

致谢

The research in this paper was supported in part by Lawrence Livermore National Laboratory, Los Alamos National Laboratory, and Sandia National Laboratory under contract B520714. We also thank the industrial sponsors of the Storage Systems Research Center, including Hewlett Packard, IBM, Intel, LSI Logic, Microsoft, ONStor, Overland Storage, and Veritas.

本文的研究部分由劳伦斯利弗莫尔国家实验室、洛斯阿拉莫斯国家实验室和桑迪亚国家实验室根据合同号 B520714 提供支持。我们还要感谢存储系统研究中心的行业赞助商，包括惠普、IBM、英特尔、LSI Logic、微软、ONStor、Overland Storage 和 Veritas。

参考

[1] A. Adya, W. J. Bolosky, M. Castro, R. Chaiken, G. Cermak, J. R. Douceur, J. Howell, J. R. Lorch, M. Theimer, and R. Wattenhofer. FARSITE: Federated, available, and reliable storage for an incompletely trusted environment. In Proceedings of the 5th Symposium on Operating Systems Design and Implementation (OSDI), Boston, MA, Dec. 2002. USENIX.
[2] Y. Breitbart, R. Vingralek, and G. Weikum. Load control in scalable distributed file structures. Distributed and Parallel Databases, 4(4):319–354, 1996.
[3] A. Brinkmann, K. Salzwedel, and C. Scheideler. Compact, adaptive placement schemes for non-uniform capacities. In Proceedings of the 14th ACM Symposium on Parallel Algorithms and Architectures (SPAA), pages 53–62, Winnipeg, Manitoba, Canada, Aug. 2002.
[4] S.-C. Chau and A. W.-C. Fu. A gracefully degradable declustered RAID architecture. Cluster Computing Journal, 5(1):97–105, 2002.
[5] D. M. Choy, R. Fagin, and L. Stockmeyer. Efficiently extendible mappings for balanced data distribution. Algorithmica, 16:215–232, 1996.
[6] F. Dabek, M. F. Kaashoek, D. Karger, R. Morris, and I. Stoica. Wide-area cooperative storage with CFS. In Proceedings of the 18th ACM Symposium on Operating Systems Principles (SOSP ‘01), pages 202–215, Banff, Canada, Oct. 2001. ACM.
[7] R. Devine. Design and implementation of DDH: A distributed dynamic hashing algorithm. In Proceedings of the 4th International Conference on Foundations of Data Organization and Algorithms, pages 101–114, 1993.
[8] A. Goel, C. Shahabi, D. S.-Y. Yao, and R. Zimmerman. SCADDAR: An efficient randomized technique to reorganize continuous media blocks. In Proceedings of the 18th International Conference on Data Engineering (ICDE ‘02), pages 473–482, Feb. 2002.
[9] A. Granville. On elementary proofs of the Prime Number Theorem for Arithmetic Progressions, without characters. In Proceedings of the 1993 Amalfi Conference on Analytic Number Theory, pages 157–194, Salerno, Italy, 1993.
[10] R. J. Honicky and E. L. Miller. A fast algorithm for online placement and reorganization of replicated data. In Proceedings of the 17th International Parallel & Distributed Processing Symposium (IPDPS 2003), Nice, France, Apr. 2003.
[11] D. Karger, E. Lehman, T. Leighton, M. Levine, D. Lewin, and R. Panigrahy. Consistent hashing and random trees: Distributed caching protocols for relieving hot spots on the World Wide Web. In ACM Symposium on Theory of Computing, pages 654–663, May 1997.
[12] B. Kr¨oll and P. Widmayer. Distributing a search tree among a growing number of processors. In Proceedings of the 1994 ACM SIGMOD International Conference on Management of Data, pages 265–276. ACM Press, 1994.
[13] W. Litwin, M.-A. Neimat, and D. Schneider. RP*: A family of order-preserving scalable distributed data structures. In Proceedings of the 20th Conference on Very Large Databases (VLDB), pages 342–353, Santiago, Chile, 1994.
[14] W. Litwin, M.-A. Neimat, and D. A. Schneider. LH*—a scalable, distributed data structure. ACM Transactions on Database Systems, 21(4):480–525, 1996.
[15] S. Rhea, P. Eaton, D. Geels, H. Weatherspoon, B. Zhao, and J. Kubiatowicz. Pond: the OceanStore prototype. In Proceedings of the 2003 Conference on File and Storage Technologies (FAST), pages 1–14, Mar. 2003.
[16] M. Ripeanu, A. Iamnitchi, and I. Foster. Mapping the Gnutella network. IEEE Internet Computing, 6(1):50–57, Aug. 2002.
[17] A. Rowstron and P. Druschel. Storage management and caching in PAST, a large-scale, persistent peer-to-peer storage utility. In Proceedings of the 18th ACM Symposium on Operating Systems Principles (SOSP ‘01), pages 188–201, Banff, Canada, Oct. 2001. ACM.
[18] H. Tang and T. Yang. An efficient data location protocol for self-organizing storage clusters. In Proceedings of the 2003 ACM/IEEE Conference on Supercomputing (SC ‘03), Phoenix, AZ, Nov. 2003.
[19] R. O. Weber. Information technology—SCSI object-based storage device commands (OSD). Technical Council Proposal Document T10/1355-D, Technical Committee T10, Aug. 2002.
[20] C. Wu and R. Burns. Handling heterogeneity in shared-disk file systems. In Proceedings of the 2003 ACM/IEEE Conference on Supercomputing (SC ‘03), Phoenix, AZ, Nov. 2003.
[21] Q. Xin, E. L. Miller, D. D. E. Long, S. A. Brandt, T. Schwarz, and W. Litwin. Reliability mechanisms for very large storage systems. In Proceedings of the 20th IEEE / 11th NASA Goddard Conference on Mass Storage Systems and Technologies, pages 146–156, Apr. 2003.