Ceph CRUSH 设计实现剖析

CRUSH（Controlled Replication Under Scalable Hashing）是 Ceph 存储系统中用于数据分布和复制的算法。关于 CRUSH 的论文解析参考: 译 - CRUSH: Controlled, Scalable, Decentralized Placement of Replicated Data 。CRUSH map 是 Ceph 集群中一个关键的配置组件，它定义了数据如何在集群的物理硬件上分布。 CRUSH 算法使得 Ceph 能够在无需中心化或者分布式元数据管理器的情况下，高效、可靠地进行数据复制和恢复。

一、CRUSH map 解析

CRUSH map 包含了集群的层次结构和各种规则，这些规则定义了数据应该如何在集群中分布。 CRUSH map 主要包含以下几个部分：

• Tunables : 一组可用于调整 CRUSH 算法行为的参数。
• Devices : 定义集群中所有可用的存储设备的列表。
• Types : 定义存储层次结构中的不同层级类型。
• Buckets : 组织和管理存储设备（如 OSDs ）的逻辑容器。
• Rules : 定义了数据的复制方式。

新建 crush map 相关代码:

struct crush_map* crush_create()
{
    struct crush_map* m;
    m = malloc(sizeof(*m));
    if (!m) return NULL;
    memset(m, 0, sizeof(*m));

    // 初始化配置
    set_optimal_crush_map(m);
    return m;
}

void set_optimal_crush_map(struct crush_map* map)
{
    map->choose_local_tries = 0;
    map->choose_local_fallback_tries = 0;
    map->choose_total_tries = 50;
    map->chooseleaf_descend_once = 1;
    map->chooseleaf_vary_r = 1;
    map->chooseleaf_stable = 1;
    map->allowed_bucket_algs = ((1 << CRUSH_BUCKET_UNIFORM) | 
                                (1 << CRUSH_BUCKET_LIST) | 
                                (1 << CRUSH_BUCKET_STRAW) | 
                                (1 << CRUSH_BUCKET_STRAW2));
}

相关命令:

# 查看 crush map
rm -rf crushmap.file crushmap-human.file
ceph osd getcrushmap -o crushmap.file
crushtool -d crushmap.file -o crushmap-human.file
cat crushmap-human.file

CRUSH map 示例:

# begin crush map
tunable choose_local_tries 0
tunable choose_local_fallback_tries 0
tunable choose_total_tries 50
tunable chooseleaf_descend_once 1
tunable chooseleaf_vary_r 1
tunable chooseleaf_stable 1
tunable straw_calc_version 1
tunable allowed_bucket_algs 54

# devices
device 0 osd.0 class hdd
device 1 osd.1 class hdd
device 2 osd.2 class hdd
device 3 osd.3 class hdd
device 4 osd.4 class hdd
device 5 osd.5 class hdd

# types
type 0 osd
type 1 host
type 2 chassis
type 3 rack
type 4 row
type 5 pdu
type 6 pod
type 7 room
type 8 datacenter
type 9 zone
type 10 region
type 11 root

# buckets
host node01 {
        id -3            # do not change unnecessarily
        id -4 class hdd  # do not change unnecessarily
        # weight 0.19537
        alg straw2
        hash 0  # rjenkins1
        item osd.0 weight 0.09769
        item osd.1 weight 0.09769
}
host node02 {
        id -5            # do not change unnecessarily
        id -6 class hdd  # do not change unnecessarily
        # weight 0.19537
        alg straw2
        hash 0  # rjenkins1
        item osd.2 weight 0.09769
        item osd.3 weight 0.09769
}
host node03 {
        id -7            # do not change unnecessarily
        id -8 class hdd  # do not change unnecessarily
        # weight 0.19537
        alg straw2
        hash 0  # rjenkins1
        item osd.4 weight 0.09769
        item osd.5 weight 0.09769
}
root default {
        id -1            # do not change unnecessarily
        id -2 class hdd  # do not change unnecessarily
        # weight 0.58612
        alg straw2
        hash 0  # rjenkins1
        item node01 weight 0.19537
        item node02 weight 0.19537
        item node03 weight 0.19537
}

# rules
rule replicated_rule {
        id 0
        type replicated
        step take default
        step chooseleaf firstn 0 type host
        step emit
}
# end crush map

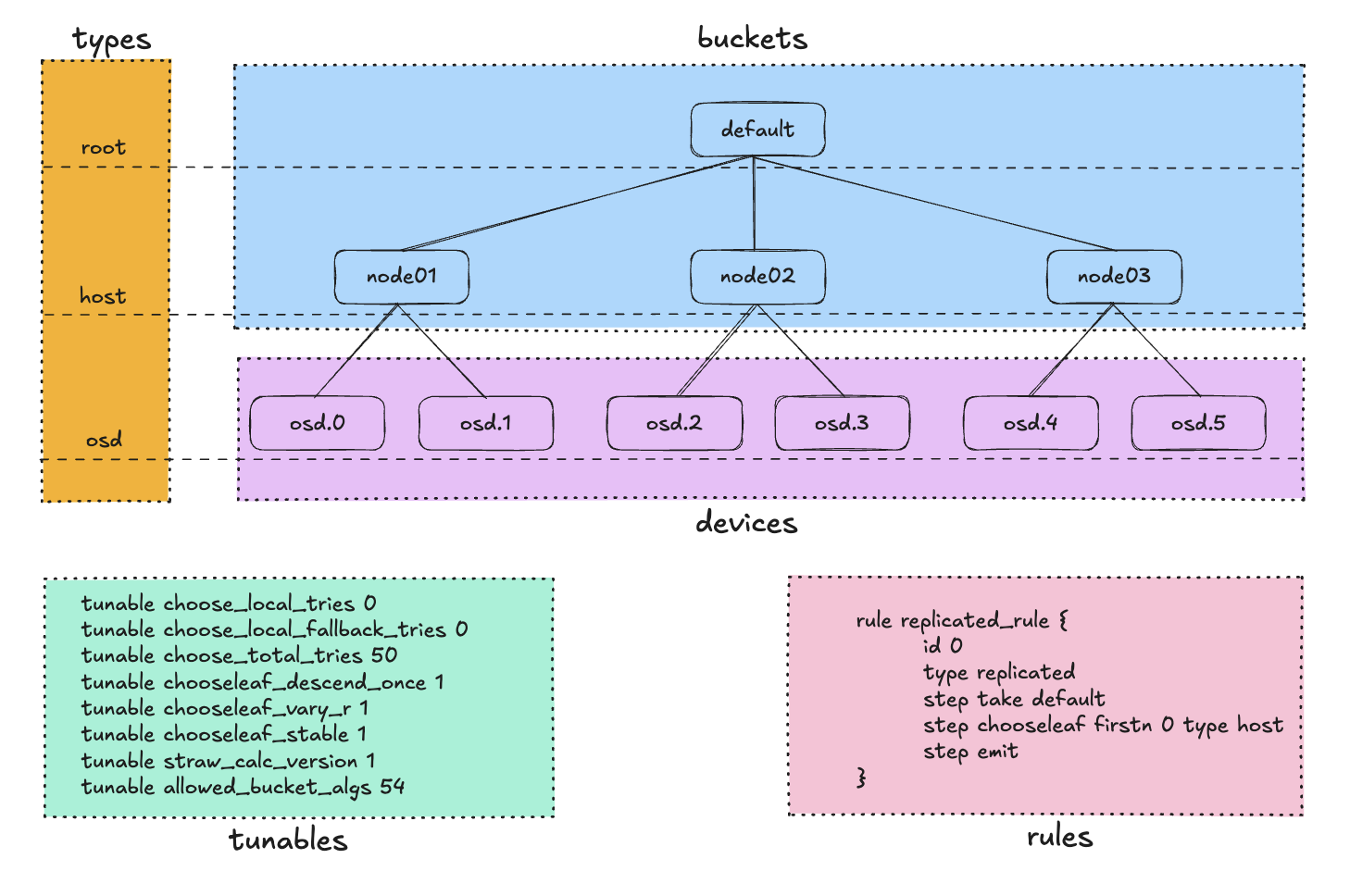
1.1、Tunables

一组可用于调整 CRUSH 算法行为的参数。通过调整这些参数，管理员可以优化数据的分布和复制策略，以适应特定的性能需求或硬件配置。

# begin crush map
tunable choose_local_tries 0
tunable choose_local_fallback_tries 0
tunable choose_total_tries 50
tunable chooseleaf_descend_once 1
tunable chooseleaf_vary_r 1
tunable chooseleaf_stable 1
tunable straw_calc_version 1
tunable allowed_bucket_algs 54

字段解析:

• choose_local_tries: 控制 CRUSH 算法在尝试找到一个本地副本（即在同一物理位置，如同一机架或同一数据中心）时的尝试次数。如果设置为 0 ，表示 CRUSH 算法不会尝试在本地找到副本。增加这个值会使算法更倾向于在本地找到副本，可能提高访问速度但减少数据分散度。
• choose_local_fallback_tries: 定义了在 choose_local_tries 未能找到本地副本后， CRUSH 算法尝试找到非本地副本之前的额外本地尝试次数。如果设置为 0 ，表示没有额外的本地回退尝试。增加这个值可以增加在本地找到副本的机会，同样可能影响数据的分散度和容错性。
• choose_total_tries: 定义了 CRUSH 算法在放弃之前尝试选择不同项的总次数。较低的值可能导致数据分布不均，而较高的值增加了计算复杂性，但可以改善数据的均匀分布。
• chooseleaf_descend_once: 控制 CRUSH 算法在选择叶节点（通常是存储设备）时是否只遍历树结构一次。设置为 1 时，算法只遍历一次，减少了计算量并提高了效率，但可能影响在复杂拓扑中的数据分布精度。
• chooseleaf_vary_r: 控制每次选择叶节点时种子是否有所变化，以增加随机性。设置为 1 时，每次选择过程的随机性增加，有助于数据的均匀分布。
• chooseleaf_stable: 确保相同的输入在 CRUSH 算法的不同版本中给出相同的输出。设置为 1 时，可以保持数据分布的一致性，特别是在升级或修改集群配置时。
• straw_calc_version: 指定使用 Straw 算法的版本， Straw 算法用于决定数据在不同存储桶之间的分配。版本 1 是较旧的版本，可能不如版本 2 在数据分布上有效和均匀。
• allowed_bucket_algs: 指定允许使用的 bucket 算法的位掩码。通过限制或启用特定的 bucket 算法，管理员可以根据具体的数据分布需求调整算法的使用，影响数据的分布和性能。

1.2、Devices

定义集群中所有可用的存储设备的列表。每个设备通常对应一个 OSD（Object Storage Daemon）。每个条目通常包含: 设备ID，OSD编号，类别。device 的 id 都是大于等于零的非负数。

# devices
device 0 osd.0 class hdd
device 1 osd.1 class hdd
device 2 osd.2 class hdd
device 3 osd.3 class hdd
device 4 osd.4 class hdd
device 5 osd.5 class hdd

1.3、Types

定义存储层次结构中的不同层级类型。

字段解析:

# types
type 0 osd         # 基本存储单元，通常对应一个物理存储设备
type 1 host        # 一台物理服务器或虚拟机，它可以包含一个或多个 osd
type 2 chassis     # 机箱或机柜，可以包含一组服务器或多个设备
type 3 rack        # 数据中心中的一个机架，通常包含多个服务器或机柜
type 4 row         # 数据中心中的一行机架
type 5 pdu         # 电源分配单元。不常见，可以用来表示依赖于同一电源单元的设备组
type 6 pod         # 表示包含多个机架或行的更大物理单元
type 7 room        # 数据中心中的一个房间，可能包含多个 pod 或行
type 8 datacenter  # 整个数据中心，是物理存储资源的大集合
type 9 zone        # 一个区域或集群的一部分
type 10 region     # 一个更大的地理区域，可能包含多个数据中心或区域
type 11 root       # CRUSH 层次结构中的最顶层，代表整个存储集群

1.4、Buckets

用来组织和管理存储设备（如 OSDs ）的逻辑容器。每个 bucket 可以包含 OSDs 或其他 buckets ，形成一个层次化的结构，这有助于定义数据在集群中的分布方式。 bucket 的设计允许 CRUSH 算法模拟物理存储的层次结构，如机架、行、数据中心等，以及在这些层次上实施数据复制和负载均衡策略。bucket 的 id 都是小于零的负数。

# buckets
host node01 {
        id -3            # do not change unnecessarily
        id -4 class hdd  # do not change unnecessarily
        # weight 0.19537
        alg straw2
        hash 0  # rjenkins1
        item osd.0 weight 0.09769
        item osd.1 weight 0.09769
}

......

root default {
        id -1            # do not change unnecessarily
        id -2 class hdd  # do not change unnecessarily
        # weight 0.58612
        alg straw2
        hash 0  # rjenkins1
        item node01 weight 0.19537
        item node02 weight 0.19537
        item node03 weight 0.19537
}

字段解析:

• host/root: bucket 类型。对应于 CRUSH 层次结构中的一个层级，如 host、rack、datacenter 等。
• node01/default: bucket 名称。通常反映其在物理或逻辑结构中的角色，如 node01、default 等。
• id: bucket id。这个 id 在 CRUSH map 中是唯一的，用于区分不同的 buckets。
• alg: bucket 算法。bucket 使用特定的算法来决定如何在其包含的项（ OSDs 或其他 buckets ）之间分配数据。常见的算法包括 uniform/list/tree/straw/straw2 。
  • uniform: 对应 CRUSH_BUCKET_UNIFORM 。一种简单的分配策略，其中所有子项都具有相同的权重，适用于所有子项具有均等的存储容量和性能的情况。
  • list: 对应 CRUSH_BUCKET_LIST 。按照列表中的顺序和指定的权重来分配数据，允许管理员精确控制数据分配的顺序，适用于需要按特定顺序优先分配数据的场景。
  • tree: 对应 CRUSH_BUCKET_TREE 。基于树形结构的数据分配方法，其中数据是按层次结构递归分配的。适用于复杂的层次结构，如多层数据中心的环境，它可以有效地在多个层级上平衡数据分布。
  • straw: 对应 CRUSH_BUCKET_STRAW 。使用一种称为 straw 算法的方法来分配数据。每个子项被赋予一个 straw ，其长度与子项的权重成比例。选择子项的概率与其 straw 的长度成正比。适用于子项之间权重差异较大的情况。
  • straw2: 对应 CRUSH_BUCKET_STRAW2 。straw 算法的改进版本，它修正了原始 straw 算法中的一些不平衡问题，提供了更加均匀和公平的数据分配。在各种场景下都能提供更好的负载均衡和数据分散性。
• hash: hash 函数。用于决定如何在 bucket 的子项之间选择。常见的哈希函数包括 rjenkins1（对应配置参数为 0 ） 。
• item: bucket 子项。这些子项可以是 OSDs（Object Storage Daemons）或者是其他的 buckets 。每个条目定义了子项的 ID 、权重以及其他可能的属性。

部分桶算法的比较:

桶算法	时间复杂度	添加	移除
uniform	O(1)	差	差
list	O(n)	优	差
straw2	O(n)	优	优

1.5、Rules

定义了数据的复制方式。例如，一个规则可能指定一个数据块应该被复制三次，并存储在不同的机架上以确保容错。

# rules
rule replicated_rule {
        id 0
        type replicated
        step take default
        step chooseleaf firstn 0 type host
        step emit
}
# end crush map

字段解析:

• rule: rule 标记。
• replicated_rule: rule name。自定义的 rule 。
• id: rule id。规则的唯一标识符。
• type: rule type。可选值为 replicated/erasure/msr_firstn/msr_indep 。
  • replicated: 最常用的规则类型，用于创建数据的多个副本。每个数据对象会在多个物理位置存储相同的副本，以提高数据的可用性和耐久性。适用于需要高数据可靠性和快速恢复能力的场景。如果一个存储节点失败，其他节点上的副本可以立即提供数据，无需复杂的恢复过程。
  • erasure: 使用纠删码技术，将数据分割成多个数据块和校验块。这种方法可以在保持相似的容错能力的同时，比简单复制更有效地使用存储空间。适用于大规模数据存储，特别是当存储成本是一个重要考虑因素时。虽然纠删码提供了高存储效率，但其恢复过程可能比复制更复杂，对性能的影响也较大。
  • msr_firstn: MSR (Multi-Site Replication) 是一种多站点复制策略，其中 FirstN 指的是在多个站点中选择前 N 个站点进行数据复制。适用于需要跨地理位置进行数据复制的场景，以实现灾难恢复和数据本地化。FirstN策略确保数据被复制到指定数量的最优站点，通常基于位置或其他标准选择。
  • msr_indep: MSR (Multi-Site Replication) 是一种多站点复制策略，其中 IndeP 指数据在每个站点独立地被复制和管理，而不是选择固定数量的站点。这种模式适用于那些需要在每个站点独立管理数据的场景，允许每个站点根据本地需求和策略来优化数据存储和访问。这种类型的复制可以提高灵活性和数据自治。
• step:
  • take: 指定了 CRUSH 算法开始选择的起点。通常，这个起点是一个 bucket ，例如一个数据中心、机架或服务器组。
  • chooseleaf: 选择方式。选择存储数据的叶子节点。叶子节点通常是指实际存储数据的设备，如硬盘或SSD。
  • choose: 选择方式。类似于 chooseleaf ，但不限于选择叶子节点。 choose 可以用于在任何级别的 bucket 中进行选择。该操作允许在非叶子级别进行更复杂的数据分布决策，例如在不同的数据中心或机架之间进行选择。
  • firstn: 选择模式。指定选择的叶子节点的数量。这个数字可以是具体的数量，也可以是 0 （表示根据复制因子自动确定数量）。常用于需要固定数量副本的场景，如在多个数据中心或机架中复制数据，确保数据的高可用性和冗余。
  • indep: 选择模式。表示每次选择都是独立的，不受之前选择的影响。这意味着即使多次执行相同的选择操作，也可能得到不同的结果。适用于需要增强随机性和分布均匀性的场景。它有助于避免因选择过程中的依赖关系而导致的数据局部化和热点问题。
  • type: 指定叶子节点的类型，如 host、rack 等，这决定了数据复制的物理分隔程度。
  • emit: 标志着选择过程的结束，输出最终确定的存储目标。

二、对象映射规则

数据对象到 OSD 的映射主要包含两个阶段:

• 对象映射到 PG：简单的哈希。
• PG 映射到 OSD 列表：CRUSH 伪随机算法。

2.1、对象映射到 PG

概要代码:

// 创建对象的定位信息
object_locator_t oloc(pool, namespacestr);

// 创建对象信息
object_t oid(objstr);

// 计算对象的原始 pg id 信息
pg_t pgid = osdmap.object_locator_to_pg(oid, oloc);

// 将对象的原始 pg id 信息转换为实际可存储的 pg 信息
// 其实是将原始 pg id 映射到 pg_num 的有效范围内
pg_t mpgid = osdmap.raw_pg_to_pg(pgid);

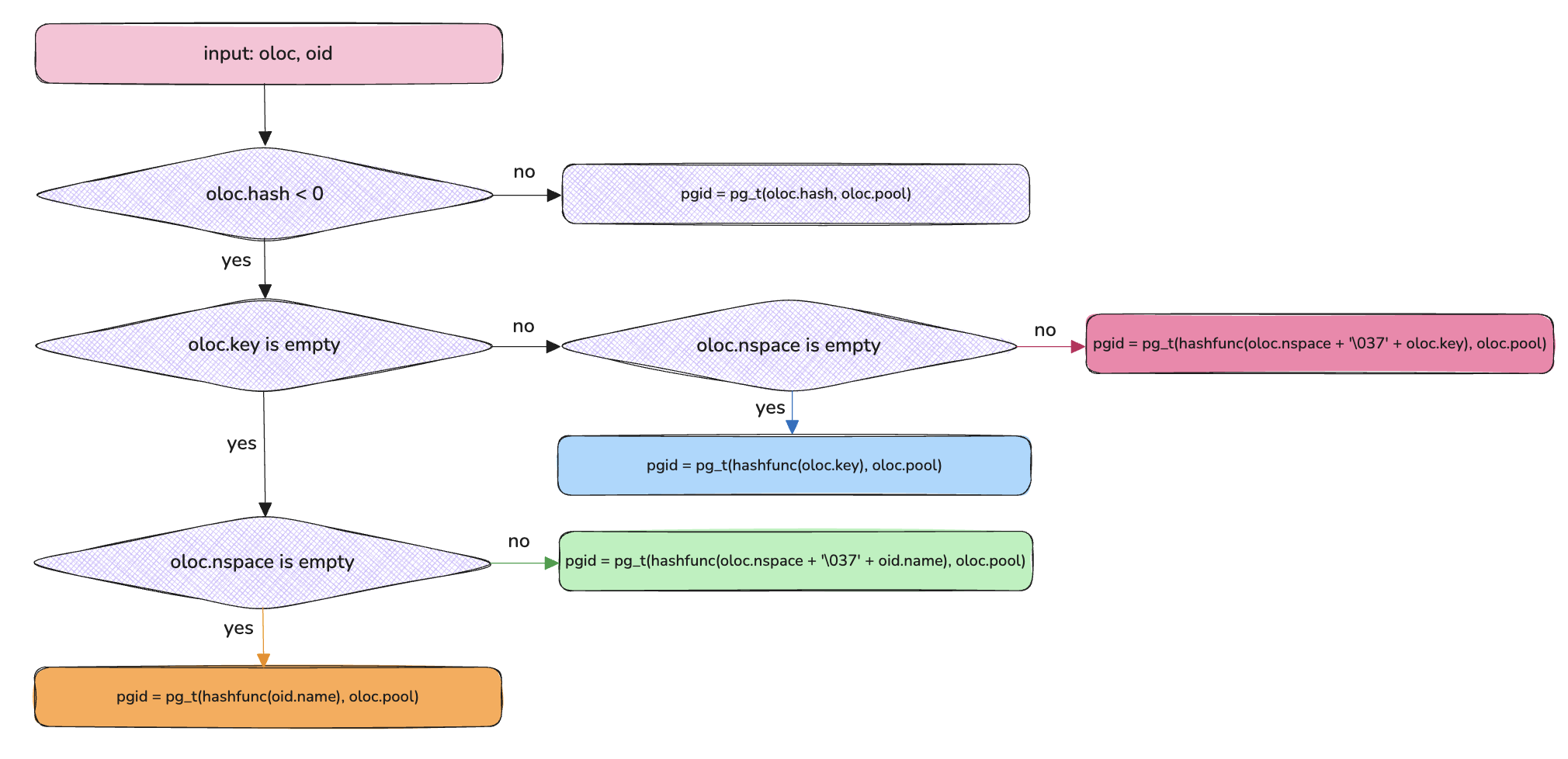
计算 pgid 的规则如下: （注意这里的 hashfunc 为特定 pool 的 hash 类型，目前支持 linux 和 rjenkins 这两种类型，默认为 rjenkins）

• 如果 oloc.hash >= 0 : 则 pgid = pg_t(oloc.hash, oloc.pool)
• 如果 oloc.hash < 0 && oloc.key 非空 && oloc.nspace 非空 : 则 pgid = pg_t(hashfunc(oloc.nspace + '\037' + oloc.key), oloc.pool)
• 如果 oloc.hash < 0 && oloc.key 非空 && oloc.nspace 为空 : 则 pgid = pg_t(hashfunc(oloc.key), oloc.pool)
• 如果 oloc.hash < 0 && oloc.key 为空 && oloc.nspace 非空 : 则 pgid = pg_t(hashfunc(oloc.nspace + '\037' + oid.name), oloc.pool)
• 如果 oloc.hash < 0 && oloc.key 为空 && oloc.nspace 为空 : 则 pgid = pg_t(hashfunc(oid.name), oloc.pool)

计算 mpgid 的规则如下:

• 规则前提: pg_num_mask 是将 pg_num 向上取到最近的二次幂数值，然后减一得到的（pgp_num 和 pgp_num_mask 关系亦如此）。比如 pg_num=16，则 pg_num_mask=15； pg_num=10，则 pg_num_mask=15；
• 计算规则:
  • 如果 (pgid.m_seed & pg_num_mask) < pg_num ， 则 mpgid.m_seed = pgid.m_seed & pg_num_mask
  • 如果 (pgid.m_seed & pg_num_mask) >= pg_num ， 则 mpgid.m_seed = pgid.m_seed & (pg_num_mask >> 1)
• 参考数值计算示例:

pgid.m_seed	pg_num	pg_num_mask	(pgid.m_seed & pg_num_mask) < pg_num	mpgid.m_seed
7	10	15	Yes	7 & 15 = 7
12	10	15	No	12 & (15 >> 1) = 4
133	16	15	Yes	133 & 15 = 5

对象映射到 PG 的相关代码实现:

struct object_t
{
    std::string name;
}

struct object_locator_t
{
    // You specify either the hash or the key -- not both
    std::int64_t pool;    // pool id
    std::string key;      // key string (if non-empty)
    std::string nspace;   // namespace
    std::int64_t hash;    // hash position (if >= 0)
}

struct pg_t
{
    uint64_t m_pool;
    uint32_t m_seed;
}

pg_t OSDMap::object_locator_to_pg(const object_t& oid, const object_locator_t& loc) const
{
    pg_t pg;
    int ret = object_locator_to_pg(oid, loc, pg);
    ceph_assert(ret == 0);
    return pg;
}

int OSDMap::object_locator_to_pg(const object_t& oid, const object_locator_t& loc, pg_t& pg) const
{
    if (loc.hash >= 0) {
        if (!get_pg_pool(loc.get_pool())) {
            return -ENOENT;
        }
        pg = pg_t(loc.hash, loc.get_pool());
        return 0;
    }
    return map_to_pg(loc.get_pool(), oid.name, loc.key, loc.nspace, &pg);
}

// mapping
int OSDMap::map_to_pg(int64_t poolid, const string& name, const string& key, const string& nspace, pg_t* pg) const
{
    // calculate ps (placement seed)
    const pg_pool_t* pool = get_pg_pool(poolid);
    if (!pool) return -ENOENT;
    ps_t ps;
    if (!key.empty())
        ps = pool->hash_key(key, nspace);
    else
        ps = pool->hash_key(name, nspace);
    *pg = pg_t(ps, poolid);
    return 0;
}

pg_t pg_pool_t::raw_pg_to_pg(pg_t pg) const
{
    pg.set_ps(ceph_stable_mod(pg.ps(), pg_num, pg_num_mask));
    return pg;
}

static inline int ceph_stable_mod(int x, int b, int bmask)
{
    if ((x & bmask) < b)
        return x & bmask;
    else
        return x & (bmask >> 1);
}

void pg_pool_t::calc_pg_masks()
{
    pg_num_mask = (1 << cbits(pg_num - 1)) - 1;
    pgp_num_mask = (1 << cbits(pgp_num - 1)) - 1;
}

2.2、PG 映射到 OSD 列表

根据上一步生成的 pgid 信息，之后利用 CRUSH 伪随机算法，便可以计算出最终映射的 osd 列表。 注意：虽然 rule 存在 replicated 和 erasure 等不同的类型，但是关键的计算 osd 列表的逻辑都是相同的，只是在处理可用 osd 列表的顺序时，逻辑有些不同，具体实现可以参考 OSDMap::_raw_to_up_osds 函数。

部分关键函数:

void crush_finalize(struct crush_map* map)
void OSDMap::_pg_to_up_acting_osds(...)
void OSDMap::_pg_to_raw_osds(...)
void CrushWrapper::do_rule(...)
int crush_do_rule(...)
size_t crush_work_size(...)
void crush_init_workspace(...)
static int crush_msr_do_rule(...)
static int crush_do_rule_no_retry(...)
static int crush_choose_firstn(...)
static void crush_choose_indep(...)
static int crush_bucket_choose(...)
static int bucket_uniform_choose(...)
static int bucket_list_choose(...)
static int bucket_tree_choose(...)
static int bucket_straw_choose(...)
static int bucket_straw2_choose(...)

2.2.1、数组空间初始化

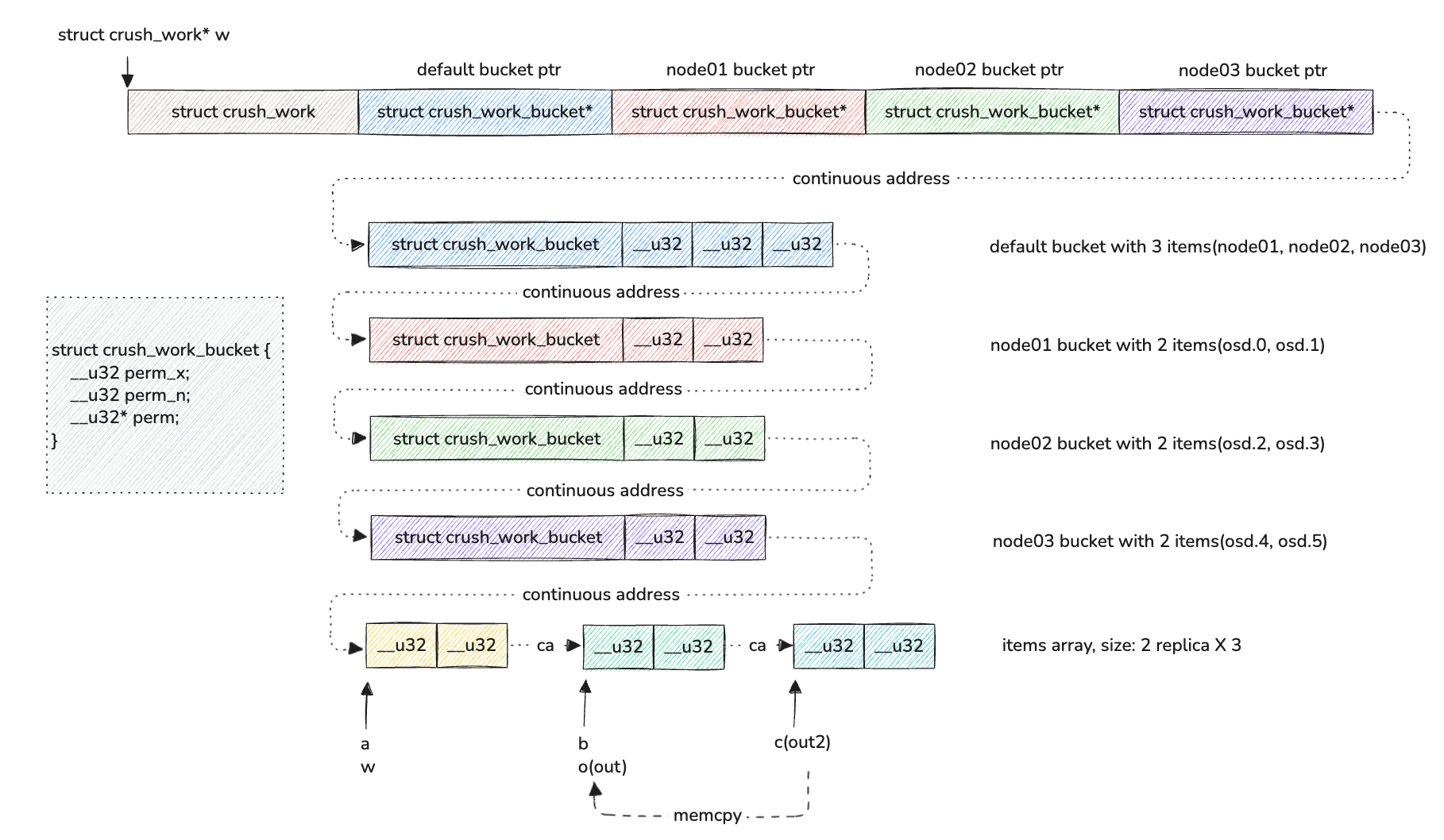
当通过 CRUSH 计算出最终的 osd 列表前，我们需要现在准备存储 osd 的空间，该空间对应的是一个 char 数组，对应代码为 char work[crush_work_size(crush, maxout)] 。在计算 osd 列表的时候会传入两个数组变量，一个是 out ，另一个是 out2 ，其中 out 用于存储非叶子节点的 item ，out2 用于存储叶子节点的 item 。

相关函数如下:

// 当所有的 bucket 被添加到 crush map 之后，会调用该函数设置 map->working_size 的大小
void crush_finalize(struct crush_map* map)

// 获取数组长度
size_t crush_work_size(const struct crush_map* map, int result_max)

// 初始化数组中 crush_work_bucket 结构体成员变量
void crush_init_workspace(const struct crush_map* m, void* v)

假设 crush map 的构成信息图如上最开始所示，则其对应的 work 数组空间如下所示:

2.2.2、获取OSD主流程

关键函数如下:

void OSDMap::_pg_to_raw_osds(const pg_pool_t& pool, pg_t pg, vector<int>* osds, ps_t* ppps) const
{
    // placement ps
    ps_t pps = pool.raw_pg_to_pps(pg);

    // size: pool 副本数量
    unsigned size = pool.get_size();

    // 获取对应 crush role id
    int ruleno = pool.get_crush_rule();

    // pps 是后面使用的 x 参数
    if (ruleno >= 0) crush->do_rule(ruleno, pps, *osds, size, osd_weight, pg.pool());

    // 移除不存在的 OSDs
    _remove_nonexistent_osds(pool, *osds);

    if (ppps) *ppps = pps;
}

// maxout 对应 pool 设置的副本数量
template<typename WeightVector>
void do_rule(int rule, int x, std::vector<int>& out, int maxout, const WeightVector& weight, uint64_t choose_args_index) const
{
    int rawout[maxout];
    char work[crush_work_size(crush, maxout)];
    crush_init_workspace(crush, work);

    // arg_map 用于 straw2 算法
    crush_choose_arg_map arg_map = choose_args_get_with_fallback(choose_args_index);
    int numrep = crush_do_rule(crush, rule, x, rawout, maxout, std::data(weight), std::size(weight), work, arg_map.args);
    if (numrep < 0) numrep = 0;
    out.resize(numrep);
    for (int i = 0; i < numrep; i++) out[i] = rawout[i];
}

int crush_do_rule(const struct crush_map* map, int ruleno, int x, int* result, int result_max, const __u32* weight,
                  int weight_max, void* cwin, const struct crush_choose_arg* choose_args)
{
    const struct crush_rule* rule;

    if ((__u32)ruleno >= map->max_rules) {
        dprintk(" bad ruleno %d\n", ruleno);
        return 0;
    }

    rule = map->rules[ruleno];
    if (rule_type_is_msr(rule->type)) {
        // 处理 CRUSH_RULE_TYPE_MSR_FIRSTN 和 CRUSH_RULE_TYPE_MSR_INDEP 类型的 rule
        return crush_msr_do_rule(map, ruleno, x, result, result_max, weight, weight_max, cwin, choose_args);
    }
    else {
        // 处理 CRUSH_RULE_TYPE_REPLICATED 和 CRUSH_RULE_TYPE_ERASURE 类型的 rule
        return crush_do_rule_no_retry(map, ruleno, x, result, result_max, weight, weight_max, cwin, choose_args);
    }
}

crush_do_rule_no_retry 函数内部会针对不同的 step 执行不同的操作，详细如下:

• CRUSH_RULE_SET_CHOOSE_TRIES: 对应操作为 step set_choose_tries ；
• CRUSH_RULE_SET_CHOOSELEAF_TRIES: 对应操作为 step set_choose_local_tries ， 会覆盖 chooseleaf_descend_once 参数， 相关的参数还有 choose_total_tries ；
• CRUSH_RULE_SET_CHOOSE_LOCAL_TRIES: 对应操作为 step set_choose_local_tries ，对应配置为 choose_local_tries ；
• CRUSH_RULE_SET_CHOOSE_LOCAL_FALLBACK_TRIES: 对应操作为 step set_choose_local_fallback_tries ，对应配置为 choose_local_fallback_tries ；
• CRUSH_RULE_SET_CHOOSELEAF_VARY_R: 对应操作为 step set_chooseleaf_vary_r，对应配置为 chooseleaf_vary_r ；
• CRUSH_RULE_SET_CHOOSELEAF_STABLE: 对应操作为 step set_chooseleaf_stable， 对应配置为 chooseleaf_stable ；
• CRUSH_RULE_TAKE: 对应操作为 step take ；
• CRUSH_RULE_CHOOSELEAF_FIRSTN: 对应操作为 step chooseleaf firstn ；
• CRUSH_RULE_CHOOSE_FIRSTN: 对应操作为 step choose firstn ；
• CRUSH_RULE_CHOOSELEAF_INDEP: 对应操作为 step chooseleaf indep ；
• CRUSH_RULE_CHOOSE_INDEP: 对应操作为 step choose indep ；
• CRUSH_RULE_EMIT: 对应操作为 step emit ；

2.2.3、Choose Firstn 逻辑

当 step 操作方式为 chooseleaf firstn 或者 choose firstn 时，会执行到 crush_choose_firstn 函数的处理逻辑中，这种方式意味着会选择前 N 个符合条件的元素。

示例 rule:

# rules
rule replicated_rule {
        id 0
        type replicated
        step take default
        step chooseleaf firstn 0 type host
        step emit
}

选择 item 的伪代码总结:

选择 item 的详细代码解析:

/**
 * crush_choose_firstn - 选择给定类型的 numrep 个不同项目
 * @map: 对应 crush map
 * @work:
 * @bucket: item 所归属的 bucket
 * @weight:
 * @weight_max:
 * @x: 输入哈希值，对应为 pgp seed
 * @numrep: crush rule 中单个 step 定义的要选择的 item 数量
 * @type: crush rule 中单个 step 定义的要选择的 item 类型
 * @out: 选中的 item 的数组
 * @outpos: 选中的 item 要存储在 out 数组中的索引
 * @out_size: 待选择的 item 的数量，计算规则为 pool 的副本数量减去已选择的 item 的数量
 * @tries: 默认为 choose_total_tries + 1 ， 默认为 51
 * @recurse_tries: 递归 chooseleaf 尝试的次数
 * @local_retries: 对应 choose_local_tries 配置，默认为 50
 * @local_fallback_retries: 对应 choose_local_fallback_tries 配置，默认为 0
 * @recurse_to_leaf: 是否递归到叶子节点
 * @vary_r: 对应 chooseleaf_vary_r 配置，默认为 1
 * @stable: 对应 chooseleaf_stable 配置，默认为 1
 * @out2: 第二个输出向量用于叶 item （如果 @recurse_to_leaf）
 * @parent_r: 从父级传递的 r 值
 * @choose_args:
 */
static int crush_choose_firstn(
    const struct crush_map* map, struct crush_work* work, const struct crush_bucket* bucket,
    const __u32* weight, int weight_max, int x, int numrep, int type, int* out, int outpos,
    int out_size, unsigned int tries, unsigned int recurse_tries, unsigned int local_retries,
    unsigned int local_fallback_retries, int recurse_to_leaf, unsigned int vary_r,
    unsigned int stable, int* out2, int parent_r, const struct crush_choose_arg* choose_args)
{
    // rep 代表 replication ，对应副本 id
    int rep;
    unsigned int ftotal, flocal;
    int retry_descent, retry_bucket, skip_rep;
    const struct crush_bucket* in = bucket;
    int r;
    int i;
    int item = 0;
    int itemtype;
    int collide, reject;
    int count = out_size;

    // ...

    // 循环遍历选择 item
    //
    // stable 默认为 1 , 因此 rep 范围为 [0, numrep) , 含义为逐步获取 numrep 个副本 item
    // count 为待选择的 item 数量，范围为 pool 的副本数量减去已选择的 item 的数量
    for (rep = stable ? 0 : outpos; rep < numrep && count > 0; rep++) {
        // 总失败次数
        ftotal = 0;

        // 是否跳过当前副本
        skip_rep = 0;

        do {
            // retry_descent 是一个标志变量，用于控制是否需要重新尝试选择过程，但这次是在更深层次的桶结构中。
            // "descent" 在这里指的是在 CRUSH 桶的层次结构中向下进行，即从当前桶向下到其子桶中进行选择。
            retry_descent = 0;

            // 记录当前 bucket
            in = bucket;

            // 重置当前 bucket 中的失败次数
            flocal = 0;

            do {
                // 是否发生了碰撞，即选择了重复的 item
                collide = 0;

                // 是否在当前 bucket 中重试
                retry_bucket = 0;

                // rep 是当前的副本编号，表示正在尝试选择第几个副本。在 CRUSH
                // 算法中，每个数据副本都应该尽可能分布在不同的设备上，以提高数据的耐用性和可用性。 parent_r
                // 是从父调用（如果有的话）传递下来的一个值，它可能代表了上一层级选择过程中的某些状态或者迭代次数。
                // 这个值的传递有助于保持选择的连贯性和上下文相关性，特别是在递归调用中。
                // 第一次调用 crush_choose_firstn 的时候，传入的 parent_r 为 0
                r = rep + parent_r;

                // ftotal
                // 是到目前为止总的失败次数，即在当前选择过程中已经尝试并失败的次数。这包括因为冲突、类型不匹配或其他原因导致的选择失败。
                // 通过将 ftotal 加到 r 上，CRUSH
                // 算法在每次失败后修改选择的种子，这有助于在下一次尝试中改变选择的结果，从而尝试避免之前导致失败的情况。
                // 这是一种常见的技术，用于在保持随机性的同时解决潜在的重复冲突或选择死锁。
                r += ftotal;

                //当前 bucket 中 item 数量为 0 ，则停止在当前 bucket 中寻找 item
                if (in->size == 0) {
                    reject = 1;
                    goto reject;
                }

                // local_fallback_retries 表示本地回退重试的次数，默认为 0 。 
                //
                // flocal >= (in->size >> 1): flocal
                // 是本地失败的次数，这个条件检查是否失败次数已经达到或超过了桶大小的一半。 flocal >
                // local_fallback_retries: 检查本地失败次数是否超过了设定的本地回退重试次数。
                if (local_fallback_retries > 0 && flocal >= (in->size >> 1) && flocal > local_fallback_retries)
                    // 如果上述条件全部满足，说明常规的选择方法可能不适用，需要使用一种备用的选择方法。
                    // 这是备用的选择方法，用于在常规方法失败后尝试另一种可能的选择方式。这个函数可能是基于某种特定的置换或者排列算法来选择设备。
                    item = bucket_perm_choose(in, work->work[-1 - in->id], x, r);
                else
                    // 从指定 bucket 中选择 item
                    // in 为 bucket
                    // x 为输入哈希值，对应为 pgp seed
                    // choose_args 为 straw2 算法需要使用的参数
                    // outpos 为待选择出的 item 在 out 数组中的索引
                    item = crush_bucket_choose(
                        in, work->work[-1 - in->id], x, r, (choose_args ? &choose_args[-1 - in->id] : 0), outpos);

                // 选择的 item 的 id 大小异常，则结束当前 rep 的 for 循环，将 rep++ 之后，进入下一个选择逻辑
                if (item >= map->max_devices) {
                    dprintk("   bad item %d\n", item);
                    skip_rep = 1;
                    break;
                }

                // item 的 id 小于 0 ，代表这是一个 bucket ， 则获取对应 bucket 的类型信息，
                // 否则当前 item 是 osd 类型 ，因此其 type 类型值为 0 。
                if (item < 0)
                    itemtype = map->buckets[-1 - item]->type;
                else
                    itemtype = 0;
                dprintk("  item %d type %d\n", item, itemtype);

                // 当前 item 的类型与期望的类型不同
                if (itemtype != type) {
                    // item >= 0 时，意味着当前 item 是一个叶子节点，此时类型仍然不匹配，基于 rep
                    // 的选择已经没有意义，尝试进入下一个 rep++ 的选择逻辑。
                    // item 为负数时，并且对应 bucket 的类型超限，则非法，结束基于当前 rep 的选择逻辑，尝试进入下一个
                    // rep++ 的选择逻辑。
                    if (item >= 0 || (-1 - item) >= map->max_buckets) {
                        dprintk("   bad item type %d\n", type);
                        skip_rep = 1;
                        break;
                    }

                    // 当前 item 不是叶子节点，则会从当前 item 对应的 bucket 中继续寻找 item
                    // 有点类似于深度遍历的逻辑。
                    in = map->buckets[-1 - item];
                    retry_bucket = 1;
                    continue;
                }

                // 走到这里意味着找到了类型匹配的 item ，但是我们需要监测该 item 是否之前已经被选择过。
                // 如果之前被选择过了，意味着发生了冲突。
                for (i = 0; i < outpos; i++) {
                    if (out[i] == item) {
                        collide = 1;
                        break;
                    }
                }

                // 没有碰撞冲突，且需要递归到叶子节点
                // 如果没有发生冲突，并且需要递归到叶子节点
                reject = 0;
                if (!collide && recurse_to_leaf) {
                    // 如果当前 item 不是叶子节点
                    if (item < 0) {
                        int sub_r;
                        // vary_r 对应 chooseleaf_vary_r 配置，默认为 1
                        if (vary_r) {
                            // 当 vary_r 为 1 时， sub_r = r
                            sub_r = r >> (vary_r - 1);
                        }
                        else {
                            sub_r = 0;
                        }

                        // 返回的值小于等于 outpos ，意味着在内部调用的时候没有找到符合条件的 item
                        if (crush_choose_firstn(
                                map,                       // 对应 crush map
                                work,                      // 
                                map->buckets[-1 - item],   // 当前 item 的 bucket
                                weight,                    // 
                                weight_max,                // 
                                x,                         // 输入哈希值，对应为 pgp seed
                                stable ? 1 : outpos + 1,   // stable 对应 chooseleaf_stable 配置，默认为 1
                                0,               // 期望的 item 类型，0 代表着叶子节点 osd 的类型
                                out2,            // 将获取的叶子节点的 item 存入 out2 数组
                                outpos,          // 期望选中的 item 在 out 数组中的索引位置
                                count,           // 
                                recurse_tries,   // 
                                0,               // 
                                local_retries,   // 对应 choose_local_tries 配置，默认为 50
                                local_fallback_retries,   // 对应 choose_local_fallback_tries 配置，默认为 0
                                0,                        // 是否递归到叶子节点
                                vary_r,                   // vary_r 对应 chooseleaf_vary_r 配置，默认为 1
                                stable,                   // stable 对应 chooseleaf_stable 配置，默认为 1
                                NULL,         // 设置传入的 out2 数组为 NULL ，因为不会使用该变量
                                sub_r,        // 按照默认值的情况， sub_r = r
                                choose_args   // choose_args 为 straw2 算法需要使用的参数
                                ) <= outpos) {
                            // 经过深度遍历的调用后，仍然没有找到新的 item ，则拒绝
                            reject = 1;
                        }
                    }
                    else {
                        // 当前 item 已经是一个叶子节点了，则将该 item 记录到 out2 数组中
                        out2[outpos] = item;
                    }
                }

                // 如果没有被拒绝，并且，也没有发生冲突
                if (!reject && !collide) {
                    // itemtype 为 0 意味着选择的 item 是一个 osd
                    if (itemtype == 0) reject = is_out(map, weight, weight_max, item, x);
                }

            reject:
                // 处理被拒绝或者发生了碰撞冲突的情况
                //
                // reject 对应的场景如下:
                // 1. 当前的 bucket 中 item 数量为 0 ，则拒绝在当前 bucket 中选择；
                // 2. 在选择叶子节点的过程中，如果没有找到符合条件的 item ，则拒绝在当前 bucket 中选择；
                //
                // collide 对应的场景如下:
                // 1. 当前选择的 item 与之前选择过的 item 一致，即发生了碰撞冲突；
                if (reject || collide) {
                    // 调整失败数量
                    ftotal++;
                    flocal++;

                    // 发生了碰撞冲突，但是在当前 bucket 中重试的次数没有超过限制，则可以再次重试。
                    // local_retries 对应 choose_local_tries 配置，默认为 50 。
                    if (collide && flocal <= local_retries) retry_bucket = 1;

                    // local_fallback_retries 对应 choose_local_fallback_tries 配置，默认为 0
                    else if (local_fallback_retries > 0 && flocal <= in->size + local_fallback_retries)
                        retry_bucket = 1;

                    // 如果总失败次数小于 tries ， 则尝试向下寻找
                    // tries 默认为 choose_total_tries + 1 ， 即默认为 51
                    else if (ftotal < tries)
                        retry_descent = 1;

                    else
                        // 放弃当前 rep 的选择
                        skip_rep = 1;

                    dprintk("  reject %d  collide %d  ftotal %u  flocal %u\n", reject, collide, ftotal, flocal);
                }
                // 在当前 bucket 中重新选择。
                //
                // 对应的场景如下:
                // 1. 当前选择的 item 的类型不是期望的类型，但其仍是一个 bucket ，可从该 bucket 中继续检索；
                // 2. 如果选择的 item 之前已经选择过，即发生了碰撞冲突，但本地失败的次数仍然在 local_retries
                //    范围内，则可以继续在当前 bucket 中重新选择；
                // 3. 如果启用了本地回退重试，且本地失败的次数满足条件，则可以继续在当前 bucket 中重新选择；
            } while (retry_bucket);

            // 下降重试。
            //
            // 对应的场景如下:
            // 1. 如果总的失败次数小于 tries ， 则可以继续下降重试
        } while (retry_descent);

        // 经过上述判断，结论是需要跳过当前 rep 的选择。
        //
        // 对应的场景如下:
        // 1. 选择的 item 异常。item 的 id 超过 max_devices 值。
        // 2. 选择的 item 类型不匹配。找到的叶子节点与期望的 item type 不匹配；找到的 item id 超过了 max_buckets值；
        // 3. 异常选择的次数不满足约束。选择过程被拒绝或者发生了碰撞冲突，且失败的次数不满足约束。
        if (skip_rep) {
            dprintk("skip rep\n");
            continue;
        }

        // 选择到符合条件的 item ，将其加入 out 数组
        dprintk("CHOOSE got %d\n", item);
        out[outpos] = item;
        outpos++;
        count--;
#ifndef __KERNEL__
        if (map->choose_tries && ftotal <= map->choose_total_tries) map->choose_tries[ftotal]++;
#endif
    }

    // 返回 out 数组中已选中 item 的数量
    dprintk("CHOOSE returns %d\n", outpos);
    return outpos;
}

2.2.4、Choose Indep 逻辑

示例 rule:

# rules
rule replicated_rule {
        id 0
        type replicated
        step take default
        step chooseleaf indep 0 type host
        step emit
}

选择 item 的伪代码总结:

选择 item 的详细代码解析:

/**
 * crush_choose_indep - 选择给定类型的 numrep 个不同项目
 * @map: 对应 crush map
 * @work:
 * @bucket: item 所归属的 bucket
 * @weight:
 * @weight_max:
 * @x: 输入哈希值，对应为 pgp seed
 * @left: 在当前 bucket 中还需要选择的 item 的数量
 * @numrep: crush rule 中单个 step 定义的要选择的 item 数量
 * @type: crush rule 中单个 step 定义的要选择的 item 类型
 * @out: 选中的 item 的数组
 * @outpos: 选中的 item 要存储在 out 数组中的索引
 * @tries: 默认为 choose_total_tries + 1 ， 默认为 51
 * @recurse_tries: 由于 choose_leaf_tries 默认为 0 ，所以该值默认为 1
 * @recurse_to_leaf: 是否递归到叶子节点
 * @out2: 第二个输出向量用于叶 item （如果 @recurse_to_leaf）
 * @parent_r: 从父级传递的 r 值
 * @choose_args: choose_args 为 straw2 算法用到的参数
 */
static void crush_choose_indep(const struct crush_map* map, struct crush_work* work,                            // 2
                               const struct crush_bucket* bucket, const __u32* weight, int weight_max, int x,   // 6
                               int left, int numrep, int type, int* out, int outpos, unsigned int tries,        // 12
                               unsigned int recurse_tries, int recurse_to_leaf, int* out2, int parent_r,        // 16
                               const struct crush_choose_arg* choose_args)                                      // 17
{
    const struct crush_bucket* in = bucket;
    int endpos = outpos + left;
    int rep;
    unsigned int ftotal;
    int r;
    int i;
    int item = 0;
    int itemtype;
    int collide;

    // ...

    // 初始化剩余所有要获取的 item 的元素在数组中的索引位置
    for (rep = outpos; rep < endpos; rep++) {
        out[rep] = CRUSH_ITEM_UNDEF;
        if (out2) out2[rep] = CRUSH_ITEM_UNDEF;
    }

    // 限制总的失败次数，并且监测在当前 bucket 中待选择的 item 数量
    for (ftotal = 0; left > 0 && ftotal < tries; ftotal++) {
#ifdef DEBUG_INDEP
        if (out2 && ftotal) {
            dprintk("%u %d a: ", ftotal, left);
            for (rep = outpos; rep < endpos; rep++) { dprintk(" %d", out[rep]); }
            dprintk("\n");
            dprintk("%u %d b: ", ftotal, left);
            for (rep = outpos; rep < endpos; rep++) { dprintk(" %d", out2[rep]); }
            dprintk("\n");
        }
#endif
        // 不断循环监测 out 数组中哪个位置上仍没有选取的 item ，则开始执行选取操作
        for (rep = outpos; rep < endpos; rep++) {
            if (out[rep] != CRUSH_ITEM_UNDEF) continue;

            // 标记当前 bucket
            in = bucket;

            // 不断循环检索
            //
            // 结束循环的条件:
            // 1. bucket 中 item 数量为空
            // 2. 选择的 item 类型为 osd ，但其 id 超过 max_devices ，则异常
            // 3. 选择的 item 为 bucekt ，但是其 id 大于 max_buckets ，则异常
            // 4. 选择 item 发生了冲突，即找到了重复的 item
            // 5. 在需要递归检索叶子节点的时候，找不到对应的叶子节点
            // 6. itemtype == 0 && is_out(map, weight, weight_max, item, x) 的情况
            // 7. 找到符合条件的 item
            for (;;) {
                // 更新 r 值
                r = rep + parent_r;

                // 如果 bucket 算法为 CRUSH_BUCKET_UNIFORM 则执行特殊处理
                if (in->alg == CRUSH_BUCKET_UNIFORM && in->size % numrep == 0)
                    r += (numrep + 1) * ftotal;
                else
                    // 更新 r 值，这是关键点，防止每次 r 值不变，找到的都是相同的 item
                    r += numrep * ftotal;

                // bucket 中元素为空，则跳过当前 bucket
                if (in->size == 0) {
                    dprintk("   empty bucket\n");
                    break;
                }

                // 根据 bucket 内配置的算法不同，执行不同的选取 item 操作
                item = crush_bucket_choose(
                    in, work->work[-1 - in->id], x, r, (choose_args ? &choose_args[-1 - in->id] : 0), outpos);

                // item 的索引大于最大的 device 则为异常，将对应的副本序号的数设置为 CRUSH_ITEM_NONE
                if (item >= map->max_devices) {
                    dprintk("   bad item %d\n", item);
                    out[rep] = CRUSH_ITEM_NONE;
                    if (out2) out2[rep] = CRUSH_ITEM_NONE;
                    left--;
                    break;
                }

                // 获取当前 item 的类型
                if (item < 0)
                    itemtype = map->buckets[-1 - item]->type;
                else
                    itemtype = 0;
                dprintk("  item %d type %d\n", item, itemtype);

                // 类型不匹配则继续寻找
                if (itemtype != type) {
                    // item 已经为叶子节点，此时类型仍然不匹配，则无法继续向下寻找，因此结束当前流程。
                    // item 并不是叶子节点，但是其 bucket id 大于 max_buckets ，意味着这是一个异常的
                    // bucket，也结束当前流程。
                    if (item >= 0 || (-1 - item) >= map->max_buckets) {
                        dprintk("   bad item type %d\n", type);
                        out[rep] = CRUSH_ITEM_NONE;
                        if (out2) out2[rep] = CRUSH_ITEM_NONE;
                        left--;
                        break;
                    }

                    // 从当前 item 的 bucket 中继续往下寻找
                    in = map->buckets[-1 - item];
                    continue;
                }

                // 监测是否发生冲突，即是否找到相同的 item
                collide = 0;
                for (i = outpos; i < endpos; i++) {
                    if (out[i] == item) {
                        collide = 1;
                        break;
                    }
                }

                // 如果存在冲突，则跳出当前循环
                if (collide) break;

                // 是否需要递归检索到叶子节点
                if (recurse_to_leaf) {
                    // 当前 item 非叶子节点
                    if (item < 0) {
                        // 继续往下一层检索
                        crush_choose_indep(
                            map,
                            work,
                            map->buckets[-1 - item],   // @bucket: 下一次要检索的 bucket
                            weight,
                            weight_max,
                            x,   // @x: 输入哈希值，对应为 pgp seed
                            1,   // @left: 在当前 bucket 中还需要选择的 item 的数量，只需要找到一个叶子节点即可
                            numrep,   // @numrep: crush rule 中单个 step 定义的要选择的 item 数量
                            0,   // @type: crush rule 中单个 step 定义的要选择的 item 类型，这里为 osd 类型
                            out2,   // @out: 选中的 item 的数组，由于这里是叶子节点，所以存入 out2 数组
                            rep,             // @outpos: 选中的 item 要存储在数组中的索引
                            recurse_tries,   // @tries: 这里传入的值为 recurse_tries 的值
                            0,               // @recurse_tries: 这里传入的值为 0
                            0,               // @recurse_to_leaf: 这里传入的值为 0
                            NULL,   // @out2: 第二个输出向量用于叶 item，由于当前检索的就是叶子节点，所以该值为 0
                            r,   // @parent_r: 从父级传递的 r 值
                            choose_args);

                        if (out2 && out2[rep] == CRUSH_ITEM_NONE) {
                            // 没有找到对应的叶子节点
                            break;
                        }
                    }
                    // 当前 item 为叶子节点，直接记录该 item
                    else if (out2) {
                        out2[rep] = item;
                    }
                }

                // 叶子节点
                if (itemtype == 0 && is_out(map, weight, weight_max, item, x)) break;

                // 找到 item ，跳出当前循环
                out[rep] = item;
                left--;
                break;
            }
        }
    }


    // 再次处理结果数组，如果内部还是未定义的 item ，则将其设置为 None
    for (rep = outpos; rep < endpos; rep++) {
        if (out[rep] == CRUSH_ITEM_UNDEF) { out[rep] = CRUSH_ITEM_NONE; }
        if (out2 && out2[rep] == CRUSH_ITEM_UNDEF) { out2[rep] = CRUSH_ITEM_NONE; }
    }
#ifndef __KERNEL__
    if (map->choose_tries && ftotal <= map->choose_total_tries) map->choose_tries[ftotal]++;
#endif
#ifdef DEBUG_INDEP
    if (out2) {
        dprintk("%u %d a: ", ftotal, left);
        for (rep = outpos; rep < endpos; rep++) { dprintk(" %d", out[rep]); }
        dprintk("\n");
        dprintk("%u %d b: ", ftotal, left);
        for (rep = outpos; rep < endpos; rep++) { dprintk(" %d", out2[rep]); }
        dprintk("\n");
    }
#endif
}

三、Bucket 算法详解

不同类别的算法实现介绍:

• uniform: 它假定整个集群的设备容量是均匀的，并且设备数量极少变化，他不关心子设备中配置的权重，而是直接通过哈希算法将数据均匀的分布到集群中，时间复杂度 O(1)，优点是计算速度快，缺点是适用范围有限。
• list/tree: 这两种属于分治算法，问题在于各子元素的选择概率是全局相关的，所以子元素的增加、删除和权重的改变都会在一定程度上影响全局的数据分布，由此带来的数据迁移量并不是最优的。
  • list: 它会逐一检查各个元素，并根据权重确定选中对应子元素的概率，时间复杂度 O(n)，优点是在集群规模不断增加时能最小化数据迁移，缺点是移除旧节点时会导致数据重新分配。
  • tree: 它使用了二叉搜索树，让搜索到各子元素的概率与权重一致，时间复杂度 O(logn)，优点是较好适应集群规模的增减，缺点是 Ceph 实现有缺陷，不推荐使用。
• straw/straw2:
  • straw 会让所有子元素独立的互相竞争，类似于抽签机制，让子元素的签长基于权重分布，并引入一定的伪随机性，时间服复杂度为 O(n) ，由于子元素签长的计算仍然会依赖于其他子元素的权重，所以并没有能够完全解决最小数据迁移量问题。
  • straw2 的提出解决了 straw 存在的问题，在计算子元素签长时不会依赖于其他子元素的状况，保证数据分布遵循权重分布，并且在集群规模变化时拥有最佳的表现。

桶算法的比较:

桶算法	选择的时间复杂度	元素添加	元素移除
uniform	O(1)	差	差
list	O(n)	良	差
tree	O(log(n))	优	优
straw	O(n)	更优	更优
straw2	O(n)	良	良

3.1、Uniform Buckets

在大型存储系统中，通常不会单独添加某个设备（个别故障除外），而是批量添加一组设备，用于扩容或者替换寿命到的设备。因此将它们视为一个单元是很自然的。在这种情况下，uniform buckets 用于表示一组相同的设备。这样做的主要优势在于性能：CRUSH 可以在常数时间内将副本映射到桶中。如果桶的大小发生变化，则设备之间的数据将完全重新排列，就像传统的基于哈希的分发策略一样。

代码解析:

struct crush_bucket_uniform* crush_make_uniform_bucket(int hash, int type, int size, int* items, int item_weight);
int crush_add_uniform_bucket_item(struct crush_bucket_uniform* bucket, int item, int weight);
int crush_remove_uniform_bucket_item(struct crush_bucket_uniform* bucket, int item);
int crush_adjust_uniform_bucket_item_weight(struct crush_bucket_uniform* bucket, int item, int weight);
static int crush_reweight_uniform_bucket(struct crush_map* map, struct crush_bucket_uniform* bucket);


static int bucket_uniform_choose(const struct crush_bucket_uniform* bucket, struct crush_work_bucket* work, int x, int r)
{
    return bucket_perm_choose(&bucket->h, work, x, r);
}

// x 为 _pg_to_raw_osds 函数中计算出的 pps
static int bucket_perm_choose(const struct crush_bucket* bucket, struct crush_work_bucket* work, int x, int r)
{
    // 将 r 的值限制在 bucket 的大小范围内
    unsigned int pr = r % bucket->size;
    unsigned int i, s;

    // 每次需要为 x 从 bucket 中选择多个 item ， 为此我们将 x 记录到 work->perm_x 字段中，
    // 因此如果 work->perm_x 发生了变更，则代表需要为新的 x 选择 item ，需要重新计算排列。
    if (work->perm_x != (__u32)x || work->perm_n == 0) {
        dprintk("bucket %d new x=%d\n", bucket->id, x);
        work->perm_x = x;

        // 如果 pr 为 0 （即第一个副本），直接使用哈希函数计算一个索引，这是一个优化，因为大多数调用都是请求第一个副本。
        if (pr == 0) {
            s = crush_hash32_3(bucket->hash, x, bucket->id, 0) % bucket->size;
            work->perm[0] = s;
            work->perm_n = 0xffff; /* magic value, see below */
            goto out;
        }

        // 如果 pr 不为 0 ，且是新的序列，则初始化排列数组 perm ，使其包含从 0 到 bucket->size-1 的整数，
        // 并且设置当前 work 中已经选择的 item 数量为 0 。
        for (i = 0; i < bucket->size; i++) work->perm[i] = i;
        work->perm_n = 0;
    }

    // 之前处理过 pr 为 0 的情况，则当前为第二次调用
    else if (work->perm_n == 0xffff) {
        // 初始化排列数组中下标 0 之后的位置
        for (i = 1; i < bucket->size; i++) work->perm[i] = i;

        // 由于当 pr 为 0 的时候（即第一次计算 x 的排列数组的情况），已经获取了 bucket 中索引 s ，并将
        // 该值记录到 work->perm[0] （即 work->perm[0] = s ），为了避免 work->perm 数组中出现 bucket 中
        // 重复的索引，所以需要将 work->perm[s] 中记录的值设置为 bucket 的索引 0，即 work->perm[s] = 0 。
        work->perm[work->perm[0]] = 0;

        // 当前 work 中已经获取的 item 数量为 1 。
        work->perm_n = 1;
    }

    for (i = 0; i < work->perm_n; i++) dprintk(" perm_choose have %d: %d\n", i, work->perm[i]);


    // 这个条件检查当前已生成的排列长度（ work->perm_n ）是否小于或等于所需的副本位置 pr 。
    // 如果是，需要继续生成排列直到达到这个位置。
    //
    // 通过不断交换元素位置，生成一个伪随机的排列，直到生成足够长的排列以覆盖所需的副本位置 pr 。
    // 确保了数据的均匀分布和访问的随机性，是 CRUSH 算法处理数据分布的关键机制。
    while (work->perm_n <= pr) {
        // 这里 p 是当前排列的长度，即下一个要处理的排列位置。
        unsigned int p = work->perm_n;

        // 如果 p 已经是最后一个元素的位置，则没有后续元素可以与之交换，因此不执行交换。
        if (p < bucket->size - 1) {
            // 使用哈希函数 crush_hash32_3 基于桶的哈希种子、对象标识符 x 、桶的 id 和当前位置 p 计算一个哈希值。
            // 然后取模操作确定在当前位置 p 之后的哪个位置与之交换。这保证了交换的随机性和均匀性。
            i = crush_hash32_3(bucket->hash, x, bucket->id, p) % (bucket->size - p);

            // 如果 i 不为 0 （即当前位置 p 不是交换位置），则执行交换操作
            if (i) {
                unsigned int t = work->perm[p + i];
                work->perm[p + i] = work->perm[p];
                work->perm[p] = t;
            }
            dprintk(" perm_choose swap %d with %d\n", p, p + i);
        }
        // 每完成一次交换，排列长度增加 1 。
        work->perm_n++;
    }

    for (i = 0; i < bucket->size; i++) dprintk(" perm_choose  %d: %d\n", i, work->perm[i]);

    // 从排列中获取 pr 位置的索引s，然后返回 bucket->items[s] ，即为选择的桶中的条目。
    s = work->perm[pr];
out:
    dprintk(" perm_choose %d sz=%d x=%d r=%d (%d) s=%d\n", bucket->id, bucket->size, x, r, pr, s);
    return bucket->items[s];
}

3.2、List Buckets

list buckets 将其内容构建为链表，并且可以包含具有任意权重的项目。为了放置副本， CRUSH 从列表头部开始，包含最新添加的项目，并将其权重与所有剩余项目的权重之和进行比较。根据 hash(x, r, item) 的值，要么以适当的概率选择当前项目，要么该过程继续递归地沿着列表向下进行。这种方法源自 RUSHp ，将放置问题重新定义为 “最近添加的” 问题。 “是新项目，还是旧项目？” 对于不断扩展的集群来说，这是一个自然而直观的选择，要么以适当的概率将对象迁移到最新的设备，要么像以前一样保留在旧设备上。当项目添加到存储桶时，其结果是最佳的数据迁移。然而，从列表中间或尾部移除项目可能会导致大量不必要的移动，因此列表存储桶最适合于从不（或很少）收缩的情况。

RUSHp 算法大致相当于一个两级 CRUSH 层次结构，由一个包含多个 uniform buckets 的 list buckets 组成。其固定的集群表示形式排除了使用放置规则或 CRUSH 故障域来控制数据放置以增强可靠性的可能性。

代码解析:

struct crush_bucket_list* crush_make_list_bucket(int hash, int type, int size, int* items, int* weights);
int crush_add_list_bucket_item(struct crush_bucket_list* bucket, int item, int weight);
int crush_remove_list_bucket_item(struct crush_bucket_list* bucket, int item);
int crush_adjust_list_bucket_item_weight(struct crush_bucket_list* bucket, int item, int weight);
static int crush_reweight_list_bucket(struct crush_map* map, struct crush_bucket_list* bucket);


static int bucket_list_choose(const struct crush_bucket_list* bucket, int x, int r)
{
    int i;

    for (i = bucket->h.size - 1; i >= 0; i--) {
        // 这个哈希值是随机的，但是对于相同的输入总是产生相同的输出，保证了算法的确定性。
        __u64 w = crush_hash32_4(bucket->h.hash, x, bucket->h.items[i], r, bucket->h.id);

        // 哈希值与 0xffff 进行 AND 操作，将哈希值限制在一个较小的范围内（即 0 到 65535 ）。
        w &= 0xffff;
        dprintk("list_choose i=%d x=%d r=%d item %d weight %x "
                "sw %x rand %llx",
                i,
                x,
                r,
                bucket->h.items[i],
                bucket->item_weights[i],
                bucket->sum_weights[i],
                w);
        // 将结果乘以到目前为止的权重总和（ bucket->sum_weights[i] ），然后右移 16 位，进行缩小。
        // 将哈希值缩放到一个与权重总和相关的范围内。
        w *= bucket->sum_weights[i];
        w = w >> 16;

        // 如果缩小后的哈希值小于当前条目的权重，这意味着在从 0 到当前权重总和的范围内，只有当值落在当前条目
        // 的权重范围内时，条目才会被选中。因此，条目被选中的概率正比于它的权重相对于权重总和的比例。
        if (w < bucket->item_weights[i]) { return bucket->h.items[i]; }
    }

    // 如果所有条目都未被选择（理论上不应发生，除非权重配置错误），则打印错误信息，并默认返回列表中的第一个条目。
    dprintk("bad list sums for bucket %d\n", bucket->h.id);
    return bucket->h.items[0];
}

3.3、Tree Buckets

与任何链表数据结构一样，list buckets 对于较小的项目集非常高效，但对于较大的项目集可能不太适用，因为其 O(n) 运行时间可能过长。源自 RUSHt 的树形桶通过将其项目存储在二叉树中解决了这个问题。这将放置时间缩短至 O(log(n))，使其适合管理更大的设备集或嵌套桶。 RUSHt 相当于一个两级 CRUSH 层次结构，由一个包含多个 uniform bucket 的 tree buckets 组成。

tree buckets 的结构为带权二叉搜索树，其项目位于叶子节点。每个内部节点都知道其左右子树的总权重，并根据固定策略进行标记（详见下文）。为了在存储桶中选择一个项目，CRUSH 从树的根节点开始，计算输入键 x、副本数量 r、存储桶标识符以及当前树节点（最初为根节点）的标签的哈希值。将结果与左右子树的权重比进行比较，以决定接下来要访问哪个子节点。此过程重复进行，直到到达叶子节点，此时存储桶中的相关项目将被选中。只需进行 log(n) 次哈希运算和节点比较即可定位项目。

存储桶的二叉树节点采用简单的固定策略标记二进制值，以避免在树增长或收缩时标签发生变化。树中最左边的叶子节点始终标记为 “1”。每次树扩展时，旧根节点都会成为新根节点的左子节点，并且树中最左边的叶子节点始终带有标签，新的根节点的标签将旧根节点的标签向左移动一位（例如 1、10、100 等）。树右侧的标签与左侧的标签相同，只是每个值前面都添加了一个 “1” 。一旦对象被放置在特定的子树中，其最终映射将仅取决于该子树中的权重和节点标签，并且只要该子树的项目保持不变，映射就不会改变。尽管分层决策树在嵌套项目之间引入了一些额外的数据迁移，但此策略将移动保持在合理水平，同时即使对于非常大的存储桶也能提供高效的映射。

root default {
        id -1             # do not change unnecessarily
        id -2 class hdd   # do not change unnecessarily
        # weight 0.6
        alg tree
        hash 0  # rjenkins1
        item host01 weight 0.2
        item host02 weight 0.2
        item host03 weight 0.2
}

假设一个 bucket 的信息如上，则根据上面的 bucket 生成的 tree 的基础信息为，depth = 3 ，num_nodes = 8 ，生成的树结构关系如下（相关代码参见 crush_make_tree_bucket 函数）:

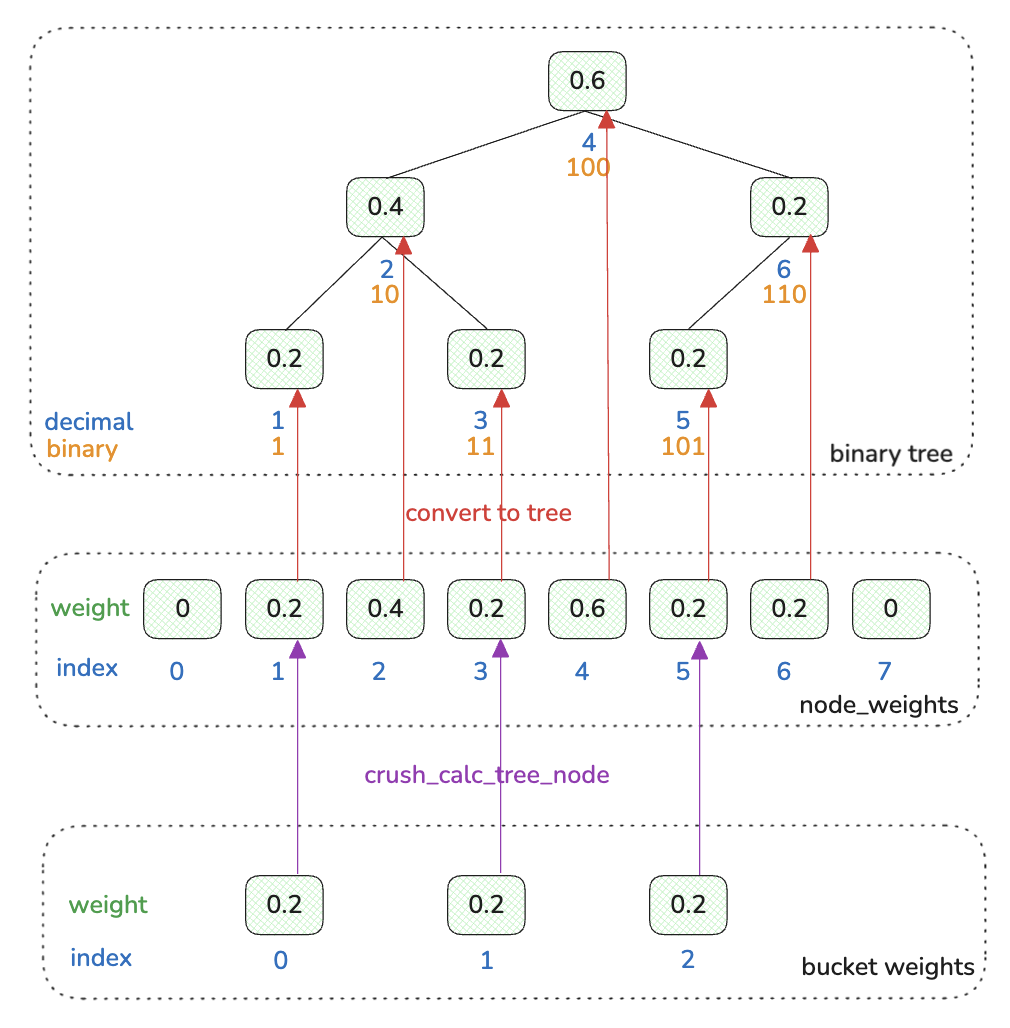
代码解析:

struct crush_bucket_tree* crush_make_tree_bucket(int hash, int type, int size, int* items, int* weights);
int crush_add_tree_bucket_item(struct crush_bucket_tree* bucket, int item, int weight);
int crush_remove_tree_bucket_item(struct crush_bucket_tree* bucket, int item);
int crush_adjust_tree_bucket_item_weight(struct crush_bucket_tree* bucket, int item, int weight);
static int crush_reweight_tree_bucket(struct crush_map* map, struct crush_bucket_tree* bucket);


/* (binary) tree */
static int height(int n)
{
    int h = 0;
    while ((n & 1) == 0) {
        h++;
        n = n >> 1;
    }
    return h;
}

// 计算给定节点 x 的左子节点的位置。这里的 h 是节点 x 的高度。
// 首先调用 height(x) 来获取 x 的高度，然后通过减去 2^(h-1) 来找到左子节点的位置。
static int left(int x)
{
    int h = height(x);
    return x - (1 << (h - 1));
}

// 计算给定节点 x 的右子节点的位置。这里的 h 是节点 x 的高度。
// 首先调用 height(x) 来获取 x 的高度，然后通过加上 2^(h-1) 来找到右子节点的位置。
static int right(int x)
{
    int h = height(x);
    return x + (1 << (h - 1));
}

// 检查节点 x 是否是一个叶子节点（即终端节点）。
// 在二进制表示中，如果最低位是 1 ，则节点是叶子节点。
static int terminal(int x)
{
    return x & 1;
}

static int bucket_tree_choose(const struct crush_bucket_tree* bucket, int x, int r)
{
    int n;
    __u32 w;
    __u64 t;

    // 从根节点开始
    n = bucket->num_nodes >> 1;

    // 如果不是叶子节点
    // 在二进制表示中，如果最低位是1，则节点是叶子节点。
    while (!terminal(n)) {
        int l;

        // 获取当前节点的权重
        w = bucket->node_weights[n];

        // 计算哈希值，然后乘以节点的权重。
        // 该哈希函数考虑了桶的哈希类型、对象ID、节点索引、随机种子和桶ID。
        t = (__u64)crush_hash32_4(bucket->h.hash, x, n, r, bucket->h.id) * (__u64)w;

        // 将 64 位结果右移 32 位，以缩减范围，使其适应权重的规模。
        t = t >> 32;

        // 计算左子节点的索引。
        l = left(n);

        // 如果计算得到的哈希值小于左子节点的权重，则选择左子节点，
        // 否则选择右子节点 (n = right(n);)。
        // 
        // 假设当前节点权重为 0.6 ， 左子节点权重为 0.4 ， 右子节点权重为 0.2 ,
        // 如果当前计算的 t 为 0.3 ，可以说明要寻找的节点位于左子节点树中；
        // 如果当前计算的 t 为 0.5 ，可以说明要寻找的节点位于右子节点树中；
        if (t < bucket->node_weights[l])
            n = l;
        else
            n = right(n);
    }

    return bucket->h.items[n >> 1];
}

3.4、Straw Buckets

list buckes 和 tree buckets 的结构使得只需计算有限数量的哈希值并将其与权重进行比较，即可选择桶中的项目。在这样做的过程中，它们会采用分治法，要么优先考虑某些项目（例如，位于列表开头的项目），要么完全无需考虑项目的整个子树。这可以提高副本放置过程的性能，但当桶的内容由于项目的添加、移除或重新调整权重而发生变化时，也可能导致重组行为不理想。

straw buckets 让所有物品都能公平 “竞争” 。通过类似于抽签的过程，每个桶中的项目都会相互竞争以放置副本。要放置副本，需要为桶中的每个项目抽取一根随机长度的签。获取最长签的项目获胜。每根签的长度最初都是一个固定范围内的值，基于 CRUSH 输入 x、副本数量 r 和桶中项目 i 的哈希值。每根签的长度都会根据项目的权重乘以因子，这样权重较大的项目更有可能获胜。虽然此过程（平均而言）几乎比 list buckets 慢两倍，甚至比 tree buckets （以对数方式缩放）更慢，但 straw buckets 在修改嵌套项目时可实现最佳数据移动。

straw buckets 的中代码在于签长的计算与选择。相关函数为 int crush_calc_straw(struct crush_map* map, struct crush_bucket_straw* bucket) 。

选择元素的相关伪代码如下:

max_x = -1
max_item = -1
for each item:
　　x = hash(input, r)
　　x = x * item_straw
　　if x > max_x
　　　　max_x = x
　　　　max_item = item
return max_item

代码解析:

struct crush_bucket_straw* crush_make_straw_bucket(struct crush_map* map, int hash, int type, int size, int* items, int* weights);
int crush_add_straw_bucket_item(struct crush_map* map, struct crush_bucket_straw* bucket, int item, int weight);
int crush_remove_straw_bucket_item(struct crush_map* map, struct crush_bucket_straw* bucket, int item);
int crush_adjust_straw_bucket_item_weight(struct crush_map* map, struct crush_bucket_straw* bucket, int item, int weight);
static int crush_reweight_straw_bucket(struct crush_map* map, struct crush_bucket_straw* bucket);


static int bucket_straw_choose(const struct crush_bucket_straw* bucket, int x, int r)
{
    __u32 i;
    int high = 0;
    __u64 high_draw = 0;
    __u64 draw;

    for (i = 0; i < bucket->h.size; i++) {
        draw = crush_hash32_3(bucket->h.hash, x, bucket->h.items[i], r);
        draw &= 0xffff;
        draw *= bucket->straws[i];
        if (i == 0 || draw > high_draw) {
            high = i;
            high_draw = draw;
        }
    }
    return bucket->h.items[high];
}

3.5、Straw2 Buckets

默认的 bucket 算法。

选择元素的相关伪代码如下:

max_x = -1
max_item = -1
for each item:
　　x = hash(input, r)
　　x = ln(x/65536) / weight
　　if x > max_x
　　　　max_x = x
　　　　max_item = item
return max_item

代码解析:

struct crush_bucket_straw2* crush_make_straw2_bucket(struct crush_map* map, int hash, int type, int size, int* items, int* weights);
int crush_add_straw2_bucket_item(struct crush_map* map, struct crush_bucket_straw2* bucket, int item, int weight);
int crush_remove_straw2_bucket_item(struct crush_map* map, struct crush_bucket_straw2* bucket, int item);
int crush_adjust_straw2_bucket_item_weight(struct crush_map* map, struct crush_bucket_straw2* bucket, int item, int weight);
static int crush_reweight_straw2_bucket(struct crush_map* map, struct crush_bucket_straw2* bucket);


static int bucket_straw2_choose(const struct crush_bucket_straw2* bucket, int x, int r, // 3
                                const struct crush_choose_arg* arg, int position) // 5
{
    unsigned int i, high = 0;
    __s64 draw, high_draw = 0;
    // 获取 bucket 中元素的权重数组。
    // 就可以通过 ceph osd crush weight-set dump 命令查看预设的 weights 信息，
    // 如果之前没有设置过 weights ，则使用 bucket 中自带的 weights 信息。
    __u32* weights = get_choose_arg_weights(bucket, arg, position);

    // 获取 bucket 中元素索引数组。
    __s32* ids = get_choose_arg_ids(bucket, arg);
    for (i = 0; i < bucket->h.size; i++) {
        dprintk("weight 0x%x item %d\n", weights[i], ids[i]);
        // 计算 bucket 中每个元素的签长。
        // 
        // 计算规则为: (2^44 * log2((hash(x, ids[i], r) & 0xffff) + 1) - 2^48) / weights[i] 。
        // 精简后的规则为: log2(hash(x, ids[i], r) & 0xffff) / weight 。
        // 
        // 从这里可以看出，从 bucket 中筛选元素的时候，仅使用 bucket 中每个元素的自身的权重，不考虑其他
        // bucket 中的元素的权重。
        if (weights[i]) { draw = generate_exponential_distribution(bucket->h.hash, x, ids[i], r, weights[i]); }
        else {
            draw = S64_MIN;
        }

        // 找到最大的签长
        if (i == 0 || draw > high_draw) {
            high = i;
            high_draw = draw;
        }
    }

    // 返回最大签长对应的元素
    return bucket->h.items[high];
}

四、数据迁移实践分析

4.1、调整 bucket 算法

相关命令:

# 获取 crush map
rm -rf crushmap.file crushmap-human.file
ceph osd getcrushmap -o crushmap.file
crushtool -d crushmap.file -o crushmap-human.file
cat crushmap-human.file

# 修改 crush map
rm -rf crushmap-modified.file
vi crushmap-human.file
crushtool -c crushmap-human.file -o crushmap-modified.file
ceph osd setcrushmap -i crushmap-modified.file

# 调整并检查 tunables 配置
# 可以将 tunables 设置为 hammer/jewel/default 
# 其中 default 指的是 jewel
# 从 hammer 开始才开始支持 straw2 算法
ceph osd crush tunables jewel
# straw_calc_version 仅支持 0 或者 1
ceph osd crush set-tunable straw_calc_version 1

# 查看 bucket 算法
ceph osd crush dump | grep alg

4.2、触发数据迁移

我们可以通过调整 osd 权重来触发数据迁移。

相关命令:

# 重新平衡数据分布
ceph osd crush reweight-all

# 备份初始 pg 分布情况
ceph pg dump pgs | awk -F ' ' '{printf "%-10s %-10s\n", $1, $17}' > oringin

# 记录原始 osd 的权重
ceph osd tree

# 调整 osd 的权重
# 下一次测试前需要重置 osd 的权重
ceph osd crush reweight osd.0 0

# 等待一会，再获取新的 pg 分布情况
ceph pg dump pgs | awk -F ' ' '{printf "%-10s %-10s\n", $1, $17}' > new

4.3、数据分析

相关命令:

# 使用下面的脚本详细分析修改前后 pg 分布的差异
./check.sh oringin new

pg 变化分析脚本:

#!/bin/bash

if [ $# -ne 2 ]; then
    echo "Usage: $0 <original_file> <new_file>"
    exit 1
fi

original_file=$1
new_file=$2

# 打印表头
printf "%-8s %-12s %-12s %-12s %-12s %-12s\n" "Line" "Origin" "New" "Removed" "Added" "OrderChanged"

# 直接处理diff命令的输出
diff "$original_file" "$new_file" -y -W 50 --suppress-common-lines | while IFS= read -r line; do
    # 提取行号
    line_number=$(echo "$line" | awk '{print $1}')

    # 提取前后的数字列表
    front_original=$(echo "$line" | grep -o '\[[^]]*\]' | head -n1)
    back_original=$(echo "$line" | grep -o '\[[^]]*\]' | tail -n1)

    front_array=($(echo "$front_original" | tr -d '[]' | tr ',' ' '))
    back_array=($(echo "$back_original" | tr -d '[]' | tr ',' ' '))

    # 初始化输出变量
    removed="-"
    added="-"
    order_changed="No"

    # 找出新增和删除的数字
    removed_nums=()
    added_nums=()
    all_numbers=$(echo "${front_array[*]} ${back_array[*]}" | tr ' ' '\n' | sort -n | uniq)
    for num in $all_numbers; do
        count_front=$(echo "${front_array[*]}" | grep -o "\b$num\b" | wc -l)
        count_back=$(echo "${back_array[*]}" | grep -o "\b$num\b" | wc -l)
        
        if (( count_front > count_back )); then
            removed_nums+=("$num")
        elif (( count_front < count_back )); then
            added_nums+=("$num")
        fi
    done

    # 设置 Removed 和 Added
    [[ ${#removed_nums[@]} -gt 0 ]] && removed="${removed_nums[*]}"
    [[ ${#added_nums[@]} -gt 0 ]] && added="${added_nums[*]}"

    # 找出在两个数组中共同存在的元素
    common_elements=()
    for num in "${front_array[@]}"; do
        if [[ " ${back_array[*]} " =~ " $num " ]]; then
            common_elements+=("$num")
        fi
    done

    # 检查共同元素的索引位置是否一致
    if [[ ${#common_elements[@]} -gt 0 ]]; then
        # 获取每个共同元素在两个数组中的索引
        for num in "${common_elements[@]}"; do
            # 在front_array中查找该元素的索引
            for ((i=0; i<${#front_array[@]}; i++)); do
                if [[ "${front_array[$i]}" == "$num" ]]; then
                    front_index=$i
                    break
                fi
            done
            
            # 在back_array中查找该元素的索引
            for ((i=0; i<${#back_array[@]}; i++)); do
                if [[ "${back_array[$i]}" == "$num" ]]; then
                    back_index=$i
                    break
                fi
            done
            
            # 如果索引位置不同，则标记为顺序变化
            if [[ "$front_index" != "$back_index" ]]; then
                order_changed="Yes"
                break
            fi
        done
    fi

    # 输出格式化结果
    printf "%-8s %-12s %-12s %-12s %-12s %-12s\n" "$line_number" "$front_original" "$back_original" "$removed" "$added" "$order_changed"
done

脚本的示例输出信息:

[root@bugwz.host crush]# ./check.sh oringin new
Line     Origin       New          Removed      Added        OrderChanged
2.38     [5,0,2]      [5,1,2]      0            1            No
2.37     [0,5,2]      [1,5,2]      0            1            No
2.35     [2,5,0]      [2,5,1]      0            1            No
2.34     [5,3,0]      [5,3,1]      0            1            No
2.30     [2,4,0]      [2,4,1]      0            1            No
2.2f     [1,3,5]      [5,3,1]      -            -            Yes
2.2d     [0,5,2]      [5,1,2]      0            1            Yes
2.2b     [2,0,4]      [2,1,4]      0            1            No
2.29     [1,3,5]      [4,3,1]      5            4            Yes
2.28     [3,0,4]      [3,4,1]      0            1            Yes
2.27     [1,3,5]      [1,3,4]      5            4            No
2.26     [5,1,2]      [5,2,1]      -            -            Yes
2.25     [2,1,5]      [2,5,1]      -            -            Yes
2.24     [1,4,3]      [1,4,2]      3            2            No
2.1f     [4,3,0]      [4,3,1]      0            1            No
3.1e     [3,0,5]      [3,4,1]      0 5          1 4          No
4.19     [0,2,5]      [5,2,1]      0            1            Yes
2.1e     [3,5,0]      [3,5,1]      0            1            No
4.18     [0,4,3]      [2,4,1]      0 3          1 2          No
3.1c     [2,0,4]      [2,1,4]      0            1            No
4.1b     [4,3,0]      [4,3,1]      0            1            No
2.1c     [0,4,2]      [1,5,2]      0 4          1 5          No
3.1d     [1,2,5]      [5,2,1]      -            -            Yes
4.1a     [4,3,0]      [4,3,1]      0            1            No
2.b      [5,0,3]      [5,2,1]      0 3          1 2          No
3.a      [5,1,2]      [5,2,1]      -            -            Yes
2.a      [5,3,0]      [5,3,1]      0            1            No
3.b      [4,0,3]      [4,3,1]      0            1            Yes
2.9      [3,4,0]      [3,4,1]      0            1            No
3.8      [4,3,0]      [4,3,1]      0            1            No
4.f      [2,4,0]      [2,4,1]      0            1            No
2.8      [0,2,5]      [1,2,5]      0            1            No
3.9      [0,2,5]      [3,1,5]      0 2          1 3          No
2.7      [4,0,3]      [4,3,1]      0            1            Yes