RedisModule剖析 - RedisBloom

RedisBloom 这个 Module 内集成了很多的小功能，其中主要包括：可扩展的布隆过滤器（BloomFilter），可扩展的布谷鸟过滤器（CuckooFilter），最小计数草图（Count-Min Sketch），近似百分位（T-Digest），头部K元素（TopK）等。

一、简介

RedisBloom 是一款集成了众多功能的 RedisModule 模块，其主要包含了 BloomFilter (布隆过滤器) ，CuckooFilter (布谷鸟过滤器)，Count-Min Sketch (最小计数草图)，T-Digest (近似百分位) 以及 TopK 功能，其中很多功能都是依据 BloomFilter类 的相关功能来进行实现的，这里将会对它们的具体实现做一下深度的剖析。

• 官网：https://redisbloom.io/
• GitHub 地址：https://github.com/RedisBloom/RedisBloom
• 命令文档地址：https://redis.io/docs/stack/bloom/
• 支持功能：
  • 可扩展的 BloomFilter (布隆过滤器) ： 用于确定一个元素是否存在于一个集群中；
  • 可扩展的 CuckooFilter (布谷鸟过滤器) ： 用于确定一个元素是否存在于一个集合中；
  • Count-Min Sketch (最小计数草图) ： 用于估计一个数据的出现次数；
  • T-Digest (近似百分位) ：
  • TopK ： 维护了 k 个最常见项目的列表；

二、可扩展的 BloomFilter (布隆过滤器)

社区在实现可扩展的 BloomFilter 的时候应该参考了论文： 《Scalable Bloom Filters》 ，这篇论文的翻译稿：

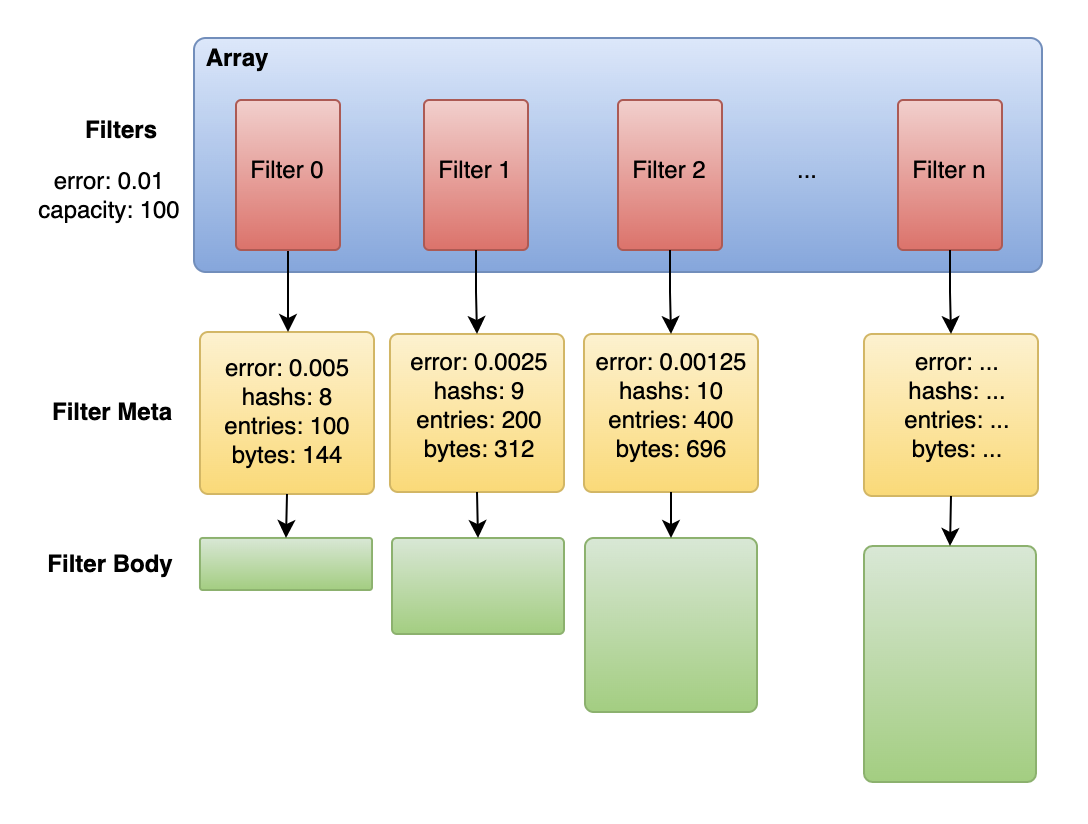
RedisBloom 通过将单个的数据表分散到多个数据表中，从而实现了一种可扩展数据表的布隆过滤器，虽然这种方式使用较为灵活，不受限于初始容量的约束，但是动态的申请多个子布隆过滤器会导致内存的增长比较严重，要这种方式就要在灵活以及内存间做一些取舍。

2.1、相关命令

以下命令仅参考当时的最新的代码，详细的准确命令请参考 社区命令文档地址 。

• bf.add : 向目标布隆过滤器中添加一个元素；
• bf.madd : 向目标布隆过滤器中添加多个元素；
• bf.exists : 在目标布隆过滤器中判断一个元素是否存在；
• bf.mexists : 在目标布隆过滤器中判断多个元素是否存在；
• bf.info : 查看对应布隆过滤器的基础信息；
• bf.debug : 查看对应布隆过滤器的详细信息（包含每个布隆过滤器表的信息）；
• bf.insert : 向目标布隆过滤器中插入元素，如果对应布隆过滤器不存在则创建；
• bf.reserve : 修改目标布隆过滤器的属性；
• bf.loadchunk : 布隆过滤器从 AOF 中加载数据时用到的命令；
• bf.scandump : 布隆过滤器向 AOF 中持久化数据时用到的命令；

2.2、编码结构

一个可扩展的布隆过滤器所依赖的主要数据结构如下所示：

typedef struct SBChain {
    SBLink *filters;  // 记录所有的布隆过滤器
    size_t size;      // 记录当前所有布隆过滤器可存储元素的数量
    size_t nfilters;  // 记录当前布隆过滤器数据的个数
    unsigned options; // 创建布隆过滤器表所依赖的参数
    unsigned growth;  // 创建新的布隆过滤器时其容量是上一个布隆过滤器的容量倍数
} SBChain;

typedef struct SBLink {
    struct bloom inner; // 对应的布隆过滤器
    size_t size;        // 已插入布隆过滤器表中的元素的个数
} SBLink;

struct bloom {
    uint32_t hashes;   // 记录当前的hash数量
    uint8_t force64;
    uint8_t n2;
    uint64_t entries;  // 记录当前布隆过滤器的容量

    double error;      // 记录当前布隆过滤器的误判率
    double bpe;

    unsigned char *bf; // 指向布隆过滤器存储内容的内存块
    uint64_t bytes;    // 记录布隆过滤器存储内容的内存块的大小（字节）
    uint64_t bits;     // 记录布隆过滤器存储内容的内存块的大小（比特）
};

2.3、哈希规则（插入/判断规则）

按照布隆过滤器的计算规则，在不同的误判率的情况下我们需要使用多个不同的哈希函数计算对应的比特位，我们接下来看一下布隆过滤器的判断/插入规则：

• 哈希算法： MurmurHash64A
• 判断方式：
  • 首先使用固定的哈希种子，对传入的元素计算其哈希值，并将其作为基础的哈希值；
  • 然后使用传入元素的哈希值作为哈希种子，计算下一次哈希位置的步进值；
  • 利用得到的传入元素的哈希特征，在多个布隆过滤器中进行判断元素是否存在；
    • 判断基础的哈希值对应的比特索引；
    • 利用计算的步进值，判断下一个对应的比特索引；

// 计算传入元素的哈希特征
bloom_hashval bloom_calc_hash64(const void *buffer, int len) {
    bloom_hashval rv;
    rv.a = MurmurHash64A_Bloom(buffer, len, 0xc6a4a7935bd1e995ULL);
    rv.b = MurmurHash64A_Bloom(buffer, len, rv.a);
    return rv;
}

// 判断多个布隆过滤器中的对应比特位
for (int ii = sb->nfilters - 1; ii >= 0; --ii) {
    if (bloom_check_h(&sb->filters[ii].inner, h)) {
        return 0;
    }
}

2.4、持久化

2.4.1、RDB的持久化

RDB 的存储过程比较简单，直接把对应结构体的所有信息持久化到 RDB 文件中，一个可扩展的布隆过滤器的存储流程如下：

• 存储对应的所有子布隆过滤器的元信息（包括子布隆过滤器的数量，配置项等）；
• 存储每个子布隆过滤器的信息：
  • 子布隆过滤器的元信息（包括元素数量，误判率，哈希数量等）；
  • 子布隆过滤器的数据信息；

2.4.2、AOF的持久化

数据 AOF 的持久化会在 AofRewrite 的时候时用到，因为需要封装一下命令以便于下一次的加载 bf.loadchunk，一个可扩展的布隆过滤器的存储流程如下：

• 首先存储对应布隆过滤器的元信息（包括布隆过滤器的数量，配置项，以及子布隆过滤器的元素数量，误判率，哈希数量等）；
  • 存储命令简化为：BF.LOADCHUNK key 1 meta_data meta_len ；
• 然后存储所有子布隆过滤器的数据信息，默认单次存储的数据信息大小最大为 16MB，以下命令会持久化多次；
  • 存储命令简化为：BF.LOADCHUNK key iter body_data body_len ；

static void BFAofRewrite(RedisModuleIO *aof, RedisModuleString *key, void *value) {
    SBChain *sb = value;
    size_t len;
    char *hdr = SBChain_GetEncodedHeader(sb, &len);
    RedisModule_EmitAOF(aof, "BF.LOADCHUNK", "slb", key, 1, hdr, len);
    SB_FreeEncodedHeader(hdr);

    long long iter = SB_CHUNKITER_INIT;
    const char *chunk;
    while ((chunk = SBChain_GetEncodedChunk(sb, &iter, &len, MAX_SCANDUMP_SIZE)) != NULL) {
        RedisModule_EmitAOF(aof, "BF.LOADCHUNK", "slb", key, iter, chunk, len);
    }
}

三、可扩展的 CuckooFilter (布谷鸟过滤器)

布谷鸟过滤器在某些场景下能够比布隆过滤器提供更好的填充率，并且支持了删除元素，在某些场景下也为很多业务提供了更好的支持。

3.1、相关命令

以下命令仅参考当时的最新的代码，详细的准确命令请参考 社区命令文档地址 。

• cf.add : 向目标布谷鸟过滤器中添加一个元素；
• cf.addnx : 向目标布谷鸟过滤器中添加一个元素，只有当元素不存在时才会添加成功；
• cf.count : 计算在目标布谷鸟过滤器中对应元素的个数，由于是计算对应元素的指纹的存在个数，因此最终结果可能不准确；
• cf.del : 从布谷鸟过滤器中删除一个元素，删除的是元素的指纹，并且只删除一次；
• cf.exists : 判断布谷鸟过滤器中对应元素是否存在；
• cf.mexists : 判断布谷鸟过滤器中多个元素是否存在；
• cf.info : 获取布谷鸟过滤器的信息；
• cf.insert : 向布谷鸟过滤器中插入一个元素，如果布谷鸟过滤器不存在则创建；
• cf.insertnx : 向布谷鸟过滤器中插入一个元素，如果布谷鸟过滤器不存在则创建，如果对应元素已经存在则不会插入成功；
• cf.reserve : 修改对应布谷鸟过滤器的属性；
• cf.loadchunk : 持久化的相关命令；
• cf.scandump : 持久化的相关命令；

3.2、编码结构

一个可扩展的布谷鸟过滤器所依赖的主要数据结构如下所示：

typedef struct {
    uint64_t numBuckets;     // bucket 的数量，大小为2次幂的值
    uint64_t numItems;       // 插入元素的数量
    uint64_t numDeletes;     // 删除元素的数量
    uint16_t numFilters;     // 所有子布谷鸟过滤器的数量
    uint16_t bucketSize;     // 每个 bucket 中可以存储指纹的数量，默认为2
    uint16_t maxIterations;  // 寻找指纹的存储空间时的最大迭代次数，默认为20次
    uint16_t expansion;      // 扩展倍数，大小为2次幂的值，默认为2
    SubCF *filters;          // 所有子布谷鸟过滤器信息的数组
} CuckooFilter;

typedef struct {
    uint32_t numBuckets;     // bucket 的数量，大小为2次幂的值
    uint8_t bucketSize;      // 每个 bucket 中可以存储指纹的数量
    uint8_t *data;           // 实际存储数据的内存块指针
} SubCF;

typedef struct {
    uint64_t i1;             // 记录元素的一个哈希值
    uint64_t i2;             // 记录元素的另一个哈希值
    uint8_t fp;              // 指纹的大小是1到255
} CuckooKey;

3.3、哈希规则（插入/判断规则）

按照布谷鸟过滤器的计算规则，当我们需要判断一个元素是否存在的时候需要判断两个位置上的空间中是否存在特定的指纹信息；当需要进行插入操作的时候需要从两个索引的位置上随机找到一个空余的空间进行插入操作，因此针对于每一个传入的元素，我们都会生成两个对应的特征值。

• 哈希算法： MurmurHash64A
• 判断方式：
  • 依据传入的元素，利用哈希算法 MurmurHash64A 计算其哈希值；
  • 利用哈希值计算对应传入元素的指纹信息(fp)，以及对应的两个哈希特征值(h1 和 h2)；
  • 依次判断多个子布谷鸟过滤器中是否有足够的空间来存储新的元素；
    • 每次都使用传入元素的两个哈希特征值（h1 和 h2）判断在对应的 bucket 的数组中是否存在空位置：
      • 如果有空位置则将对应的元素指纹插入对应空位；
      • 如果没有空位置则尝试进行踢除操作；
  • 插入元素或者判断元素是否存在结束；

// 传入元素的特征信息
typedef struct {
    uint64_t h1;
    uint64_t h2;
    uint8_t fp;
} LookupParams;

// 依据其中的一个位置来计算另一个的位置
static uint64_t getAltHash(uint8_t fp, uint64_t index) {
    return ((uint64_t)(index ^ ((uint64_t)fp * 0x5bd1e995)));
}

// 计算对应哈希值的指纹以及对应的两个位置
static void getLookupParams(uint64_t hash, LookupParams *params) {
    params->fp = hash % 255 + 1;
    params->h1 = hash;
    params->h2 = getAltHash(params->fp, params->h1);
}

uint64_t hash = MurmurHash64A_Bloom(elem, elemlen);
LookupParams params;
getLookupParams(hash, &params);

3.4、踢除规则

由于不同传入值的指纹可能相同，同一个 bucket 的空间可能会被其他相同指纹的传入值占满，导致新的值无法插入，这时就需要对已有空间中的值进行踢除操作。

• 相关函数：Filter_KOInsert
• 具体流程：
  1. 将从最新的布谷鸟过滤器中执行踢除操作；
  2. 依据传入值的其中一个哈希值，找到对应的 bucket 的位置，获取其中特定位置中的指纹信息，然后将新的指纹存储到特定位置上；
  3. 寻找上次获取到的 bucket 中的老的指纹的下一个位置点，判断对应的 bucket 中是否有空闲位置：
     1. 如果有空闲位置，则将之前替换出的指纹存到新 bucket 的空闲位置中；
     2. 如果没有空闲位置，则再次进行寻找，再次从第2步开始；

3.5、持久化

3.5.1、RDB的持久化

RDB 的存储过程比较简单，直接把对应结构体的所有信息持久化到 RDB 文件中，一个可扩展的布谷鸟过滤器的存储流程如下：

• 存储对应的所有子布谷鸟过滤器的元信息（包括子布谷鸟过滤器的数量，配置项等）；
• 存储每个子布谷鸟过滤器的信息：
  • 子布谷鸟过滤器的元信息（包括 bucket 数量等）；
  • 子布谷鸟过滤器的数据信息；

3.5.2、AOF的持久化

数据 AOF 的持久化会在 AofRewrite 的时候时用到，因为需要封装一下命令以便于下一次的加载 cf.loadchunk，一个可扩展的布谷鸟过滤器的存储流程如下：

• 首先存储对应布谷鸟过滤器的元信息（包括布谷鸟过滤器的数量，配置项，以及子布谷鸟过滤器的 bucket 数量等）；
  • 存储命令简化为：CF.LOADCHUNK key 1 meta_data meta_len ；
• 然后存储所有子布谷鸟过滤器的数据信息，默认单次存储的数据信息大小最大为 16MB，以下命令会持久化多次；
  • 存储命令简化为：CF.LOADCHUNK key iter body_data body_len ；

四、Count-Min Sketch (最小计数草图)

Count-Min Sketch (最小计数草图) 的实现思路类似于 Counting-BloomFilter (计数布隆过滤器) , 插入的过程中，使用多个哈希函数使得对应元素在对应位置上的值（范围是uint32_t）加1；查询的过程中，使用多个哈希函数获取对应元素在对应位置上的值（范围是uint32_t），并返回最小值（将其作为这个元素的操作次数），因此最终的值有可能会大于实际的操作值，Count-Min Sketch 的名字也是这么来的。

4.1、相关命令

以下命令仅参考当时的最新的代码，详细的准确命令请参考 社区命令文档地址 。

• cms.incrby : 按增量增加对应元素的计数值，支持多元素增加计算；
• cms.info : 获取对应草图的宽度、深度和总数；
• cms.initbydim : 根据指定的 width 和 depth 来初始化 Count-Min Sketch；
  • 格式 : cms.initbydim key width depth
  • 解释 :
    • key : 草图的名称；
    • width : 每个数组中计数器的数量，如果该值较小，则误判的概率较大；
    • depth : 每次需要比较的数组的数量（计数器阵列的数量），减少特定大小错误的概率（占总数的百分比）；
• cms.initbyprob : 根据错误率计算得到对应的 width 和 depth 来初始化 Count-Min Sketch；
  • 格式 : cms.initbyprob key error probability
  • 解释 :
    • key : 草图的名称；
    • error : 预估错误的值，这应该是介于 0 和 1 之间的十进制值，错误是总计数项目的百分比，影响草图的宽度；
    • probability : 膨胀计数的期望概率，这应该是介于 0 和 1 之间的十进制值（例如 0.001），影响草图的深度；
  • 计算规则 :
    • 相关函数 : CMS_DimFromProb ；
    • width 值 : ceil(2 / error) ；
    • depth 值 : ceil(log10f(probability) / log10f(0.5))；
• cms.merge : 将多个草图合并为一个草图。所有草图必须具有相同的宽度和深度，支持设置合并的权重；
• cms.query : 返回草图中一个或多个项目的计数；

4.2、编码结构

// 最小计数草图的数据结构
typedef struct CMS {
    size_t width;         // 每个数组中的计数器数，用于减小错误大小
    size_t depth;         // 计数器阵列的数量
    uint32_t *array;      // 数组指针
    size_t counter;       // 当前最小计数草图中所有元素的计数和
} CMSketch;

4.3、哈希规则

• 哈希算法： MurmurHash2 ；
• 具体流程：
  • 每一个最小计数草图都有一个深度的值，依据该深度值依次查询对应深度的对应索引上的值；
  • 根据当前的深度，设置获取哈希值的种子（从 0 到 当前最小计数草图的深度），然后得到对应的哈希值；
  • 依据哈希值得到当前深度下的对应位置上的值；
  • 获取或者变更对应位置上的值；

for (size_t i = 0; i < cms->depth; ++i) {
    uint32_t hash = MurmurHash2(item, itemlen, i);
    size_t loc = (hash % cms->width) + (i * cms->width);
    cms->array[loc] += value;
    if (cms->array[loc] < value) {
        cms->array[loc] = UINT32_MAX;
    }

    // ...

}

4.4、持久化

4.4.1、RDB的持久化

RDB 的存储过程比较简单，直接把对应结构体的所有信息持久化到 RDB 文件中，一个最小计数草图的存储流程如下：

• 存储对应的最小计数草图的元信息（包括深度，宽度，当前计数和等）；
• 存储对应的最小计数草图的数据信息（即对应结构体中的 array 指针指向的内存块信息）；

4.4.2、AOF的持久化

AOF 的存储过程没有使用自定义的命令，而直接使用了 RESTORE 命令进行持久化：

• 相关函数：RMUtil_DefaultAofRewrite；
• 具体格式：RESTORE key 0 buffer buffer_len ；

五、T-Digest (近似百分位)

T-Digest 是一个简单、快速、精确度高、可并行化的近似百分位算法，被 ElastichSearch、Spark 和 Kylin 等系统使用。TDigest 主要有两种实现算法，一种是 buffer-and-merge 算法，一种是 AVL树 的聚类算法。RedisBloom 使用的是 buffer-and-merge 算法。

5.1、相关命令

以下命令仅参考当时的最新的代码，详细的准确命令请参考 社区命令文档地址 。

• tdigest.create : 创建一个 T-Digest 草图；
• tdigest.add : 将一个或多个值添加到 T-Digest 草图；
• tdigest.reset : 清空草图并重新初始化它；
• tdigest.merge : 将多个 T-Digest 草图中的数据合并到目标 T-Digest 草图中；
• tdigest.min : 获取草图中最小的值；
• tdigest.max : 获取草图中最大的值；
• tdigest.quantile : 返回一个或多个截止值的估计值，使得添加到此 T-Digest 的观察值的指定分数将小于或等于每个指定的截止值；
• tdigest.cdf : 估计添加的所有观察值中 <= 值的比例；
• tdigest.info : 获取 T-Digest 草图的信息；
• tdigest.rank : 检索值的估计等级（草图中小于值的观察数 + 等于值的观察数的一半）；
• tdigest.revrank : 检索值的估计等级（草图中大于值的观察数 + 等于值的观察数的一半）
• tdigest.byrank : 检索具有给定等级的值的估计值；
• tdigest.byrevrank : 使用给定的反向排名检索值的估计；
• tdigest.trimmed_mean : 估计草图中的平均值，不包括低和高截止分位数之外的观察值；

5.2、编码结构

// T-Digest 数据结构
struct td_histogram {
    double compression;             // 压缩参数，默认值为100 （100 是正常使用的常用值，1000 则是一个非常大的值）
    double min;                     // 记录插入的最小的值
    double max;                     // 记录插入的最大的值
    int cap;                        // 节点的容量
    int merged_nodes;               // 节点前面的合并节点数量
    int unmerged_nodes;             // 缓冲节点（已经插入的，但是还没有进行merge的节点）的数量
    long long total_compressions;   // 执行数据压缩的次数
    double merged_weight;           // 已经merge的节点的权重值
    double unmerged_weight;         // 缓冲节点（已经插入的，但是还没有进行merge的节点）的权重和
    double *nodes_mean;             // 记录插入的节点值
    double *nodes_weight;           // 记录插入的节点的权重值
};

5.3、数据压缩

• 相关函数：
  • 判断函数：should_td_compress
  • 执行函数：td_compress
• 压缩逻辑：
  • 快速排序等待压缩的节点数组，调用 td_qsort ；
  • 其他压缩逻辑，详见函数：td_compress ；

5.4、持久化

5.4.1、RDB的持久化

RDB 的存储过程比较简单，直接把对应结构体的所有信息持久化到 RDB 文件中，一个 T-Digest 的存储流程如下：

• 尝试进行数据压缩；
• 存储对应的 T-Digest 的所有元信息（包括压缩值，最大最小值，容量，节点数等）；
• 存储对应的 T-Digest 的节点信息（已经 merge 节点的值和权重值）；

5.4.2、AOF的持久化

AOF 的存储过程没有使用自定义的命令，而直接使用了 RESTORE 命令进行持久化：

• 相关函数：RMUtil_DefaultAofRewrite；
• 具体格式：RESTORE key 0 buffer buffer_len ；

六、TopK（头部K元素）

TopK 用于展示前 K 个分数最高的数据，数据存储方式参考了 Count-Min Sketch (最小计数草图) 的设计实现，可以容纳的有效数据量依赖于初始化时指定的 width 和 depth ，并且引入了一种分数衰减机制来实现对老数据的清理。

6.1、相关命令

以下命令仅参考当时的最新的代码，详细的准确命令请参考 社区命令文档地址 。

• topk.reserve : 初始化一个 TopK；
• topk.add : 向 TopK 中添加元素，支持添加多个元素；
• topk.incrby : 按增量增加一个或多个元素的计数；
• topk.query : 检查一个或多个项目是否在 TopK 中；
• topk.count : 返回项目的计数；
• topk.list : 返回 Top K 列表中项目的完整列表;
• topk.info : 返回 TopK 的数量、宽度、深度和衰减值；

6.2、编码结构

#define TOPK_DECAY_LOOKUP_TABLE 256

typedef struct topk {
    uint32_t k;            // 要保留的常见项目的数量
    uint32_t width;        // 每个数组中保留的计数器数，默认宽度为 8
    uint32_t depth;        // 数组的数量，默认深度为 7
    double decay;          // 默认衰减系数为 0.9

    Bucket *data;          // 存储的 Bucket 的内存块指针，Bucket 数量为 width * depth
    HeapBucket *heap;      // 存储 k 个大小的 HeapBucket 数组指针，第一个最小，最后一个最大
    double lookupTable[TOPK_DECAY_LOOKUP_TABLE];  // 预计算的衰减系数的数组，容量256，值内容为：pow(decay, i)
} TopK;

typedef struct Bucket {
    uint32_t fp;           // 插入元素的指纹信息 
    counter_t count;       // 对应指纹的分数
} Bucket;

typedef struct HeapBucket {
    uint32_t fp;           // 对应元素的指纹信息
    uint32_t itemlen;      // 对应元素的原始长度
    char *item;            // 
    counter_t count;       // 对应元素的分数
} HeapBucket;

6.3、哈希规则

• 哈希算法： MurmurHash2 ；
• 具体流程：
  • 获取元素的指纹信息；
  • 依次遍历整个 TopK 的不同深度中对应索引处的值，判断数据是否存在；
    • 使用对应的深度值 i 作为哈希种子，计算对应元素的哈希值；
    • 哈希值取模 TopK 的宽度，计算出对应元素在当前深度中的索引；
    • 判断对应索引处的信息是否为插入的元素，以便于应对插入与查询操作；

// 元素指纹的计算方式
uint32_t fp = MurmurHash2(item, itemlen, 1919);

// 元素 Bucket 的计算方式
for (uint32_t i = 0; i < topk->depth; ++i) {
    uint32_t loc = MurmurHash2(item, itemlen, i) % topk->width;
    Bucket *runner = topk->data + i * topk->width + loc;

    // ...

}

6.4、TopK堆更新机制

• 触发条件：
  • 操作元素的分数值大于 TopK 中的最小值；
• 更新方式：
  • 如果对应元素已经存在：更新对应元素的分数，然后重新排序对应元素的位置直到结束的位置；
  • 如果对应元素不存在：剔除 TopK 中第一个元素，将其替换为本次变更的元素，然后对整个 TopK 进行重新排序；
• 更新细节：
  • 相关函数：heapifyDown ；

void heapifyDown(HeapBucket *array, size_t len, size_t start) {
    size_t child = start;

    // check whether larger than children
    if (len < 2 || (len - 2) / 2 < child) {
        return;
    }
    child = 2 * child + 1;
    if ((child + 1) < len && (array[child].count > array[child + 1].count)) {
        ++child;
    }
    if (array[child].count > array[start].count) {
        return;
    }

    // swap while larger than child
    HeapBucket top = {0};
    memcpy(&top, &array[start], sizeof(HeapBucket));
    do {
        memcpy(&array[start], &array[child], sizeof(HeapBucket));
        start = child;

        if ((len - 2) / 2 < child) {
            break;
        }
        child = 2 * child + 1;

        if ((child + 1) < len && (array[child].count > array[child + 1].count)) {
            ++child;
        }
    } while (array[child].count < top.count);
    memcpy(&array[start], &top, sizeof(HeapBucket));
}

6.5、衰减算法

• 衰减的考量：
  • 之前写入的老数据可能长时间不在访问，但是它们还会一直占用着对应的存储位置，如果老数据之前的分数较高，则其可能长时间位于 TopK 中；
  • 随着数据量的增加，新写入的数据可能会和被计算到与老数据相同的位置上，如果位置相同，但是指纹却不同，此时我们无法对现有的分数进行变更，但是我们可以尝试不断衰减老数据的分数，直到其为零后，我们就可以将其指纹以及分数替换成新的数据值；
  • 通过这种方式我们可以实现变化的 TopK 排行，并且解决了老数据占位的问题；
• 触发衰减的条件（必须全部满足）：
  • 执行元素插入操作，相关命令：topk.add ， topk.incrby；
  • 根据元素而计算的存储位置处非空且对应的指纹和元素的指纹不匹配；
• 衰减的机制：
  • 临时 delay 的值：
    • 对应位置的分数 小于 256 ，则值为 topk->lookupTable[count] ；
    • 对应位置的分数 大于 256 ，则值为 pow(topk->lookupTable[255], count/255 * topk->lookupTable[count%256]) ;
  • 随机值 chance ： 等于 rand() / (double)(2^32-1) ；
    • 如果随机值 chance 小于 decay 则将 原始分数减1；

uint32_t local_incr = increment;
for (; local_incr > 0; --local_incr) {
    double decay;
    if (*countPtr < TOPK_DECAY_LOOKUP_TABLE) {
        decay = topk->lookupTable[*countPtr];
    } else {
        //  using precalculate lookup table to save cpu
        decay = pow(topk->lookupTable[TOPK_DECAY_LOOKUP_TABLE - 1],
                    (*countPtr / TOPK_DECAY_LOOKUP_TABLE) *
                        topk->lookupTable[*countPtr % TOPK_DECAY_LOOKUP_TABLE]);
    }
    double chance = rand() / (double)RAND_MAX;
    if (chance < decay) {
        --*countPtr;
        if (*countPtr == 0) {
            runner->fp = fp;
            *countPtr = local_incr;
            maxCount = max(maxCount, *countPtr);
        }
    }
}

6.5、持久化

6.5.1、RDB的持久化

RDB 的存储过程比较简单，直接把对应结构体的所有信息持久化到 RDB 文件中，一个 TopK 的存储流程如下：

• 尝试进行数据压缩；
• 存储对应的 TopK 的所有元信息（包括保留分数最大的数量，数组的计数数量，数组的计数深度，衰减值等）；
• 存储对应的 TopK 的数据信息（包括所有的数据及分数信息，TopK 中的数据及其分数信息）；

6.5.2、AOF的持久化

AOF 的存储过程没有使用自定义的命令，而直接使用了 RESTORE 命令进行持久化：

• 相关函数：RMUtil_DefaultAofRewrite；
• 具体格式：RESTORE key 0 buffer buffer_len ；

七、参考链接：

• Scalable Bloom Filters
• Bloom Filter 和　Count-Min Sketch 介绍
• TDigest 算法原理
• The t-digest: Efficient estimates of distributions