Markdown中支持LaTex数学公式
一、引言
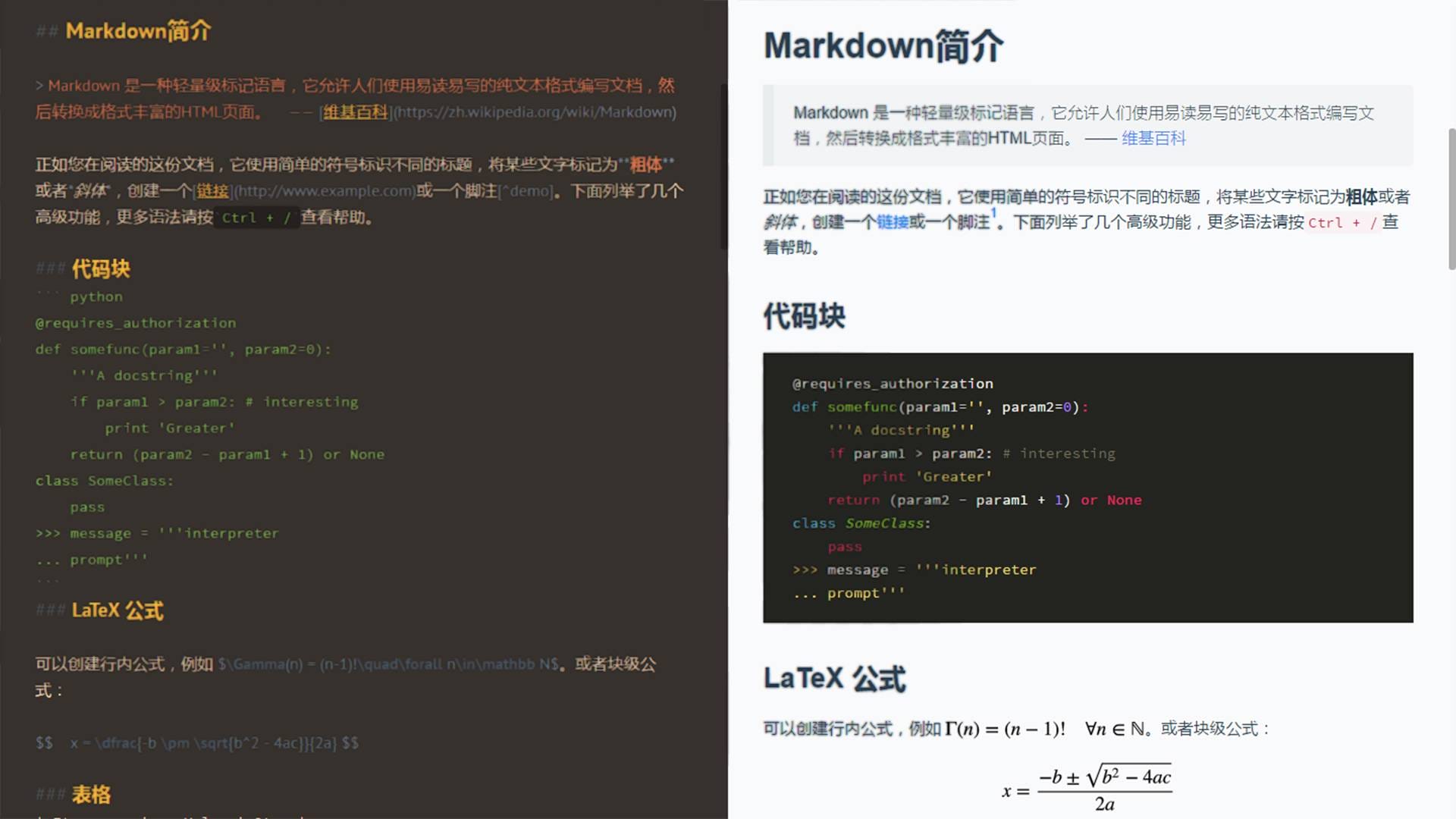
Markdown在目前无疑是一个比较好的写作方式,但是它时候和大部分的写作软件一样,在一些数据公式的编写上,只能引入图片呢?除了引用图片之外是不是还有更好的数学公式编辑手段呢?这里主要介绍一下LaTex Math在Markdown上的支持。
本博客目前采用hexo-renderer-kramed渲染器替换了Hexo自带的hexo-renderer-marked渲染器来支持LaTex;
LaTex介绍
LaTex是一种基于TeX的排版系统,LaTeX使用TeX作为它的格式化引擎,LaTeX遵循呈现与内容分离的设计理念,以便作者可以专注于他们正在编写的内容,而不必同时注视其外观。在准备LaTeX文档时,作者使用章(chapter)、节(section)、表(table)、图(figure)等简单的概念指定文档的逻辑结构,并让LaTeX系统负责这些结构的格式和布局。因此,它鼓励从内容中分离布局,同时仍然允许在需要时进行手动排版调整。这个概念类似于许多文字处理器允许全局定义整个文档的样式的机制,或使用层叠样式表来规定HTML的样式。LaTeX系统是一种可以处理排版和渲染的标记语言。
二、Markdown的Latex规则
2.1、行内与独行
行内公式:将公式插入到本行内,格式为$公式内容$,如:$xyz$,展示效果为:$xyz$;独行公式:将公式居中插入到新的一行内,格式为$$公式内容$$,如:$$xyz$$,展示效果为:$$xyz$$
2.2、上标、下标与组合
上标符号:格式为^,如:$x^4$,展示效果为:$x^4$;下标符号:格式为_,如:$x_1$,展示效果为:$x_1$;组合符号:格式为{},如:${16}_{8}O{2+}_{2}$,展示效果为:${16}{8}O{2+}{2}$;
2.3、汉字、字体与格式
汉字形式:格式为\mbox{},如:$V_{\mbox{初始}}$,展示效果为:$V_{\mbox{初始}}$;字体控制:格式为\displaystyle,如:$\displaystyle \frac{x+y}{y+z}$,展示效果为:$\displaystyle \frac{x+y}{y+z}$;下划线符号:格式为\underline,如:$\underline{x+y}$,展示效果为:$\underline{x+y}$;标签:格式为\tag{数字},如:$\tag{11}$,展示效果为:$\tag{11}$;上大括号:格式为\overbrace{算式},如:$\overbrace{a+b+c+d}^{2.0}$,展示效果为:$\overbrace{a+b+c+d}^{2.0}$;下大括号:格式为\underbrace{算式},如:$a+\underbrace{b+c}_{1.0}+d$,展示效果为:$a+\underbrace{b+c}_{1.0}+d$;上位符号:格式为\stacrel{上位符号}{基位符号},如:$\vec{x}\stackrel{\mathrm{def}}{=}{x_1,\dots,x_n}$,展示效果为:$\vec{x}\stackrel{\mathrm{def}}{=}{x_1,\dots,x_n}$;
2.4、占位符
两个quad空格:格式为\qquad,如:$x \qquad y$,展示效果为:$x \qquad y$;quad空格:格式为\quad,如:$x \quad y$,展示效果为:$x \quad y$;大空格:格式为\,如:$x \ y$,展示效果为:$x \ y$;中空格:格式为\:,如:$x : y$,展示效果为:$x : y$;小空格:格式为\,,如:$x , y$,展示效果为:$x , y$;没有空格``:格式为,如:$xy$`,展示效果为:$xy$;紧贴:格式为\!,如:$x ! y$,展示效果为:$x ! y$;
2.5、定界符与组合
括号:格式为()\big(\big) \Big(\Big) \bigg(\bigg) \Bigg(\Bigg),如:$()\big(\big) \Big(\Big)\bigg(\bigg)\Bigg(\Bigg)$,展示效果为:$()\big(\big) \Big(\Big) \bigg(\bigg) \Bigg(\Bigg)$;中括号:格式为[],如:$[x+y]$,展示效果为:$[x+y]$;大括号:格式为\{ \},如:${x+y}$,展示效果为:${x+y}$;自适应括号:格式为\left \right,如:$\left(x\right)$,$\left(x{yz}\right)$,展示效果为:$\left(x\right)$,$\left(x{yz}\right)$;组合公式:格式为{上位公式 \choose 下位公式},如:${n+1 \choose k}={n \choose k}+{n \choose k-1}$,展示效果为:${n+1 \choose k}={n \choose k}+{n \choose k-1}$;组合公式:格式为{上位公式 \atop 下位公式},如:$\sum_{k_0,k_1,\ldots>0 \atop k_0+k_1+\cdots=n}A_{k_0}A_{k_1}\cdots$,展示效果为:$\sum_{k_0,k_1,\ldots>0 \atop k_0+k_1+\cdots=n}A_{k_0}A_{k_1}\cdots$;
2.6、四则运算
加法运算:格式为符号:+,如:$x+y=z$,展示效果为:$x+y=z$;减法运算:格式为-,如:$x-y=z$,展示效果为:$x-y=z$;加减运算:格式为\pm,如:$x \pm y=z$,展示效果为:$x \pm y=z$;减甲运算:格式为\mp,如:$x \mp y=z$,展示效果为:$x \mp y=z$;乘法运算:格式为\times,如:$x \times y=z$,展示效果为:$x \times y=z$;点乘运算:格式为\cdot,如:$x \cdot y=z$,展示效果为:$x \cdot y=z$;星乘运算:格式为\ast,如:$x \ast y=z$,展示效果为:$x \ast y=z$;除法运算:格式为\div,如:$x \div y=z$,展示效果为:$x \div y=z$;斜法运算:格式为/,如:$x/y=z$,展示效果为:$x/y=z$;分式表示:格式为\frac{分子}{分母},如:$\frac{x+y}{y+z}$,展示效果为:$\frac{x+y}{y+z}$;分式表示:格式为{分子} \voer {分母},如:${x+y} \over {y+z}$,展示效果为:${x+y} \over {y+z}$;绝对值表示:格式为||,如:$|x+y|$,展示效果为:$|x+y|$;
2.7、高级运算
- 平均数运算:格式为
\overline{算式},如:$\overline{xyz}$,展示效果为:$\overline{xyz}$; - 开二次方运算:格式为
\sqrt,如:$\sqrt x$,展示效果为:; - 开方运算:格式为
\sqrt[开方数]{被开方数},如:$\sqrt[3]{x+y}$,展示效果为:$\sqrt[3]{x+y}$; - 对数运算:格式为
\log,如:$\log(x)$,展示效果为:$\log(x)$; - 极限运算:格式为
\lim,如:$\lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$,展示效果为:$\lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$; - 极限运算:格式为
\displaystyle \lim,如:$\displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$,展示效果为:$\displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$; - 求和运算:格式为
\sum,如:$\sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$,展示效果为:$\sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$; - 求和运算:格式为
\displaystyle \sum,如:$\displaystyle \sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$,展示效果为:$\displaystyle \sum^{x \to \infty}_{y \to 0}{\frac{x}{y}}$; - 积分运算:格式为
\int,如:$\int^{\infty}_{0}{xdx}$,展示效果为:$\int^{\infty}_{0}{xdx}$; - 积分运算:格式为
\displaystyle \int,如:$\displaystyle \int^{\infty}_{0}{xdx}$,展示效果为:$\displaystyle \int^{\infty}_{0}{xdx}$; - 微分运算:格式为
\partial,如:$\frac{\partial x}{\partial y}$,展示效果为:$\frac{\partial x}{\partial y}$; - 矩阵表示:格式为
\begin{matrix} \end{matrix},如:$\left[ \begin{matrix} 1 &2 &\cdots &4\5 &6 &\cdots &8\\vdots &\vdots &\ddots &\vdots\13 &14 &\cdots &16\end{matrix} \right]$,展示效果为:$\left[ \begin{matrix} 1 &2 &\cdots &4\5 &6 &\cdots &8\vdots &\vdots &\ddots &\vdots\13 &14 &\cdots &16\end{matrix} \right]$;
2.8、逻辑运算
- 等于运算:格式为
=,如:$x+y=z$,展示效果为:$x+y=z$; - 大于运算:格式为
>,如:$x+y>z$,展示效果为:$x+y>z$; - 小于运算:格式为
<,如:$x+y<z$,展示效果为:$x+y<z$; - 大于等于运算:格式为
\geq,如:$x+y \geq z$,展示效果为:$x+y \geq z$; - 小于等于运算:格式为
\leq,如:$x+y \leq z$,展示效果为:$x+y \leq z$; - 不等于运算:格式为
\neq,如:$x+y \neq z$,展示效果为:$x+y \neq z$; - 不大于等于运算:格式为
\ngeq,如:$x+y \ngeq z$,展示效果为:$x+y \ngeq z$; - 不大于等于运算:格式为
\not\geq,如:$x+y \not\geq z$,展示效果为:$x+y \not\geq z$; - 不小于等于运算:格式为
\nleq,如:$x+y \nleq z$,展示效果为:$x+y \nleq z$; - 不小于等于运算:格式为
\not\leq,如:$x+y \not\leq z$,展示效果为:$x+y \not\leq z$; - 约等于运算:格式为
\approx,如:$x+y \approx z$,展示效果为:$x+y \approx z$; - 恒定等于运算:格式为
\equiv,如:$x+y \equiv z$,展示效果为:$x+y \equiv z$;
2.9、集合运算
- 属于运算:格式为
\in,如:$x \in y$,展示效果为:$x \in y$; - 不属于运算:格式为
\notin,如:$x \notin y$,展示效果为:$x \notin y$; - 不属于运算:格式为
\not\in,如:$x \not\in y$,展示效果为:$x \not\in y$; - 子集运算:格式为
\subset,如:$x \subset y$,展示效果为:$x \subset y$; - 子集运算:格式为
\supset,如:$x \supset y$,展示效果为:$x \supset y$; - 真子集运算:格式为
\subseteq,如:$x \subseteq y$,展示效果为:$x \subseteq y$; - 非真子集运算:格式为
\subsetneq,如:$x \subsetneq y$,展示效果为:$x \subsetneq y$; - 真子集运算:格式为
\supseteq,如:$x \supseteq y$,展示效果为:$x \supseteq y$; - 非真子集运算:格式为
\supsetneq,如:$x \supsetneq y$,展示效果为:$x \supsetneq y$; - 非子集运算:格式为
\not\subset,如:$x \not\subset y$,展示效果为:$x \not\subset y$; - 非子集运算:格式为
\not\supset,如:$x \not\supset y$,展示效果为:$x \not\supset y$; - 并集运算:格式为
\cup,如:$x \cup y$,展示效果为:$x \cup y$; - 交集运算:格式为
\cap,如:$x \cap y$,展示效果为:$x \cap y$; - 差集运算:格式为
\setminus,如:$x \setminus y$,展示效果为:$x \setminus y$; - 同或运算:格式为
\bigodot,如:$x \bigodot y$,展示效果为:$x \bigodot y$; - 同与运算:格式为
\bigotimes,如:$x \bigotimes y$,展示效果为:$x \bigotimes y$; - 实数集合:格式为
\mathbb{R},如:mathbb{R},展示效果为:\mathbb{R}; - 自然数集合:格式为
\mathbb{Z},如:\mathbb{Z},展示效果为:\mathbb{Z}; - 空集:格式为
\emptyset,如:$\emptyset$,展示效果为:$\emptyset$;
2.10、数学符号
- 无穷:格式为
\infty,如:$\infty$,展示效果为:$\infty$; - 虚数:格式为
\imath,如:$\imath$,展示效果为:$\imath$; - 虚数:格式为
\jmath,如:$\jmath$,展示效果为:$\jmath$; - 数学符号:格式为
\hat{a},如:$\hat{a}$,展示效果为:$\hat{a}$; - 数学符号:格式为
\check{a},如:$\check{a}$,展示效果为:$\check{a}$; - 数学符号:格式为
\breve{a},如:$\breve{a}$,展示效果为:$\breve{a}$; - 数学符号:格式为
\tilde{a},如:$\tilde{a}$,展示效果为:$\tilde{a}$; - 数学符号:格式为
\bar{a},如:$\bar{a}$,展示效果为:$\bar{a}$; - 矢量符号:格式为
\vec{a},如:$\vec{a}$,展示效果为:$\vec{a}$; - 数学符号:格式为
\acute{a},如:$\acute{a}$,展示效果为:$\acute{a}$; - 数学符号:格式为
\grave{a},如:$\grave{a}$,展示效果为:$\grave{a}$; - 数学符号:格式为
\mathring{a},如:$\mathring{a}$,展示效果为:$\mathring{a}$; - 一阶导数符号:格式为
\dot{a},如:$\dot{a}$,展示效果为:$\dot{a}$; - 二阶导数符号:格式为
\ddot{a},如:$\ddot{a}$,展示效果为:$\ddot{a}$; - 上箭头:格式为
\uparrow,如:$\uparrow$,展示效果为:$\uparrow$; - 上箭头:格式为
\Uparrow,如:$\Uparrow$,展示效果为:$\Uparrow$; - 下箭头:格式为
\downarrow,如:$\downarrow$,展示效果为:$\downarrow$; - 下箭头:格式为
\Downarrow,如:$\Downarrow$,展示效果为:$\Downarrow$; - 左箭头:格式为
\leftarrow,如:$\leftarrow$,展示效果为:$\leftarrow$; - 左箭头:格式为
\Leftarrow,如:$\Leftarrow$,展示效果为:$\Leftarrow$; - 右箭头:格式为
\rightarrow,如:$\rightarrow$,展示效果为:$\rightarrow$; - 右箭头:格式为
\Rightarrow,如:$\Rightarrow$,展示效果为:$\Rightarrow$; - 底端对齐的省略号:格式为
\ldots,如:$1,2,\ldots,n$,展示效果为:$1,2,\ldots,n$; - 中线对齐的省略号:格式为
\cdots,如:$x_1^2 + x_2^2 + \cdots + x_n^2$,展示效果为:$x_1^2 + x_2^2 + \cdots + x_n^2$; - 竖直对齐的省略号:格式为
\vdots,如:$\vdots$,展示效果为:$\vdots$; - 斜对齐的省略号:格式为
\ddots,如:$\ddots$,展示效果为:$\ddots$;
2.11、希腊字母
| 字母 | 格式实现 | 字母 | 格式实现 |
|---|---|---|---|
| A | A |
α | \alhpa |
| B | B |
β | \beta |
| Γ | \Gamma |
γ | \gamma |
| Δ | \Delta |
δ | \delta |
| E | E |
ϵ | \epsilon |
| Z | Z |
ζ | \zeta |
| H | H |
η | \eta |
| Θ | \Theta |
θ | \theta |
| I | I |
ι | \iota |
| K | K |
κ | \kappa |
| Λ | \Lambda |
λ | \lambda |
| M | M |
μ | \mu |
| N | N |
ν | \nu |
| Ξ | \Xi |
ξ | \xi |
| O | O |
ο | \omicron |
| Π | \Pi |
π | \pi |
| P | P |
ρ | \rho |
| Σ | \Sigma |
σ | \sigma |
| T | T |
τ | \tau |
| Υ | \Upsilon |
υ | \upsilon |
| Φ | \Phi |
ϕ | \phi |
| X | X |
χ | \chi |
| Ψ | \Psi |
ψ | \psi |
| Ω | \v |
ω | \omega |
三、目前使用的问题
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 咕咕!
评论